Dear Aspirants, the most awaited notification of SBI PO – 2019 has been released. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5905]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Direction (1 – 5): Study the following information carefully and answer the given questions:
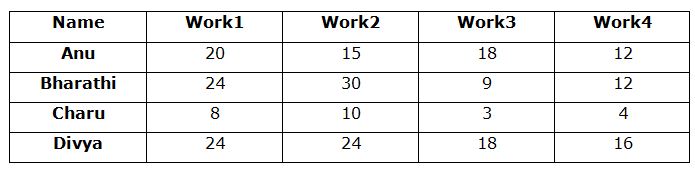
Four different types of works viz. work1, work2, work3 and work4. The following information gives the number of days taken by four different persons to complete the particular work alone.
Anu: She takes to complete the work1, work2, work3 and work4 in 20 days, 15 days, 18 days and 12 days respectively.
Bharathi: Bharathi can complete the work1 in 24 days. Bharathi and Anu together can complete the work2, work3 in 10 days and 6 days respectively. She takes 12 days to complete the work4.
Charu: Efficiency of Charu is 3 time the efficiency of Bharathi.
Divya: Divya and Charu together can complete the work1 in 6 days. She takes 12 days to complete the work1 and work2 together. Bharathi and Divya together can complete the work3 in 6 days. Divya takes 16 days to complete the work4.
1) In how many days can Soni alone complete the work3?
Quantity I: In work3, Anu and Bharathi started working together but Anu left after 2 days. After another 2 days Soni joined Bharathi and they complete the work in 3 more days.
Quantity II: Charu, Soni and Divya together can complete the work3 in 2 days.
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
2) Charu, Anu and Divya planned to complete work2 together but Anu left after 2 days and Divya left the work on 3 days before the completion of the work. Charu continued to complete the whole work. If Charu’s per day wages is Rs.200, find the wages received by Charu for completion of work2?
a) Rs.1600
b) Rs.1800
c) Rs.1400
d) Rs.1200
e) None of these
3) Bharathi is 80% more efficient than Ram. In how many days can complete work2 if Bharathi and Ram working together?
a) 19(2/7) days
b) 17(2/7) days
c) 13(2/7) days
d) 23(2/7) days
e) None of these
4) If Anu has worked for 2 days, Bharathi worked for 3 days, Charu worked for 2 days and Divya worked for some days to complete the work1. The ratio of number of days Charu and Bharathi worked to complete work4 is 1:2, and Anu and Divya worked for 2 days to complete work4. The number of days which Divya have worked on work1 is approximately what percent of the number of days which Bharathi have worked on work4?
a) 370%
b) 380%
c) 375%
d) 385%
e) None of these
5) Anu and Charu worked together for some days Charu left the work1. If Anu completed the remaining work1 in 6 days, for how many days did Charu work?
a) 2 days
b) 3 days
c) 4 days
d) 5 days
e) None of these
Directions (6 – 10): Each question below contains a statement followed by Quantity I and Quantity II. Find both to find the relationship among them. Mark your answer accordingly.
6) Quantity I: Train P started from station VGH towards station PTR with the speed of 36 Km/h at the same time train Q started from station AWD towards station STP with the speed of 40 Km/h. All the four stations are in a straight line from east to west in the order VGH, AWD, PTR and STP and distance between the consecutive stations is same i.e. 540 Km. Find the distance between train P and train Q after 5 hours.
Quantity II: Train M started from station ABC towards station PQR at 6:00 PM. After one hour train N started from station XYZ towards station PQR. All the three stations are in a straight line such that station PQR is between station ABC and station XYZ. Distance between ABC and PQR is 480 Km and distance between ABC and XYZ is 1020 Km. If the speed of train M and train N are 32 Km/h and 44 Km/h respectively, find the distance between two trains at 9:00 PM.
a) Quantity I < Quantity II
b) Quantity I ≤ Quantity II
c) Quantity I > Quantity II
d) Quantity I ≥ Quantity II
e) Quantity I = Quantity II or Relation cannot be determined
7) Quantity I: Find the value of x : 46 x 54 ÷ 26 x 15 = 75 x 53 x 8x
Quantity II: Find the value of y: 104 x 42 ÷ 28 = (25)2 x 4y
a) Quantity I < Quantity II
b) Quantity I ≤ Quantity II
c) Quantity I > Quantity II
d) Quantity I ≥ Quantity II
e) Quantity I = Quantity II or Relation cannot be determined
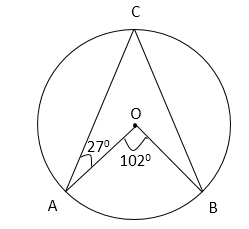
8) Quantity I: Find the value of ∠OBC
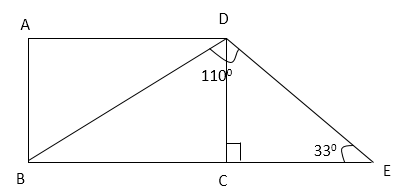
Quantity II: Find the value of ∠DBC.
a) Quantity I < Quantity II
b) Quantity I ≤ Quantity II
c) Quantity I > Quantity II
d) Quantity I ≥ Quantity II
e) Quantity I = Quantity II or Relation cannot be determined
9) Quantity I: Ajay, Subho and Jawed entered partnership with investment of Rs.45000, Rs.75000 and Rs.60000 respectively. After 8 months, Ajay doubled his investment. After two more months, Jawed left the partnership. At the end of one year, they earned a total profit of Rs.222000. Find the share of Subho in the profit.
Quantity II: Preeti, Amitabh and Suman started a business with investment in the ratio 8:6:7 respectively. After one year, Amitabh made his investment 1.5 times. After one more year, Preeti withdrew half of his investment. At the end of three years, they earned a total profit Rs.325000. Find share of Suman in the profit.
a) Quantity I < Quantity II
b) Quantity I ≤ Quantity II
c) Quantity I > Quantity II
d) Quantity I ≥ Quantity II
e) Quantity I = Quantity II or Relation cannot be determined
10) Quantity I: A 108 litres mixture of milk and water contains milk and water in the ratio 5:4 respectively. The mixture is divided in two gallons in the 7:5. The milkman added 10 litres more water in the first gallon and 5 litres more water in the second gallon. Find the difference between quantities of water in both the gallons.
Quantity II: A 72 litres mixture of wine and water contains wine and water in the ratio 3:1 respectively. A person added 10 litres more wine and 8 litres more water to the mixture. Another person added a 36 litres mixture of wine and water which contains wine and water in the ratio 1:1 to the mixture. Find the difference between the quantities of wine and water in the final mixture.
a) Quantity I < Quantity II
b) Quantity I ≤ Quantity II
c) Quantity I > Quantity II
d) Quantity I ≥ Quantity II
e) Quantity I = Quantity II or Relation cannot be determined
Answers :
Direction (1 – 5):
Anu:
Work1=1/20
Work2=1/15
Work3=1/18
Work4=1/12
Bharathi:
Work1=1/24
(Anu and Bharathi) work2=1/10
Bharathi work2=1/10-1/15=1/30
Bharathi Work3=1/6-1/18=2/18=1/9
Work 4=1/12
Charu:
Work1=3/24=1/8
Work2=3/30=1/10
Work3=3/9=1/3
Work4=3/12=1/4
Divya:
Work1=1/6-1/8=1/24
Work2=1/12-1/24=1/24
Work3=1/6-1/9=1/18
Work4=1/16
1) Answer: a)
From Quantity I:
Anu and Bharathi’s one day work = (1/18) + (1/9) = (3/18) = 1/6
Anu and Bharathi’s two days work = (1/6)*2 = 1/3
Remaining work = 1 – 1/3 = 2/3
Bharathi’s two days work = 2/9
Remaining = 2/3 – 2/9 = 4/9
Soni and Bharathi complete the work in another 3 more days. So,
(4/9)*(Soni + Bharathi’s whole work) = 3
Soni + Bharathi’s whole work = 3*(9/4) = 27/4
Soni’s one day work = (4/27) – (1/9) = 1/27
Soni alone can complete the work in 27 days.
From quantity II,
Charu + Soni + Divya = 1/2
Soni=1/2-1/3-1/18=(9-6-1)/18=1/9
Soni complete the work in 9 days.
2) Answer: c)
According to the question,
x/10 + 2/15+ (x-3)/24=1
12x+16+5x-15=120
17x=119
x=7
Charu works in 7 days, so her wages is 200*7=Rs.1400
3) Answer: a)
Ram can finish the work2 in=30*180/100=54 days
Ram and Bharathi can finish the work2 in=1/30+1/54
=(9+5)/270
=14/270
=270/14 days
=19(2/7) days
4) Answer: a)
Work1:
2/20+3/24+2/8+x/24=1
12+15+30+5x=120
5x=63
x=63/5
Work4:
Charu and Bharathi work for y and 2y days respectively.
2/12+2y/12+y/4+2/16=1
24+24y+36y+18=144
60y=102
y=17/10
Bharathi=2y=(17/10)*2=17/5
Required percentage= (63/5)*100 / (17/5)=6300/17=370%
5) Answer: c)
(x+6)/20+x/8=1
8x+48+20x=160
28x=112
x=4 days
Direction (6-10) :
6) Answer: a)
Quantity I:
Distance travelled by train P in 5 hours = 36 x 5 = 180 Km
Distance travelled by train Q in 5 hours = 40 x 5 = 200 Km

Required distance = 540 – 180 + 200 = 560 Km
Quantity II:
Distance between station PQR and station XYZ = 1020 – 480 = 540 Km
Distance travelled by train M in 3 hours = 32 x 3 = 96 km
Distance travelled by train N in 2 hours = 44 x 2 = 88 Km
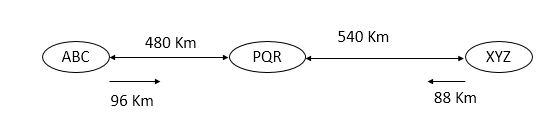
Required distance = 480 + 540 – 96 – 88 = 836 Km
Hence, Quantity I < Quantity II
7) Answer: c)
Quantity I:
(22)6 x 54 ÷ 26 = 5 x 53 x (23)x
=> (2)(12 – 6)= (2)3x
=> 6 = 3x
=> x = 2
Quantity II:
54 x 24 x (22)2 ÷ 28 = (52)2 x (22)y
=> 54 x 2(4 + 4 – 8) = 54 x 22y
=> 20 = 22y
=> 2y = 0
=> y = 0
Hence, Quantity I > Quantity II
8) Answer: a)
Find the value of ∠OBC.
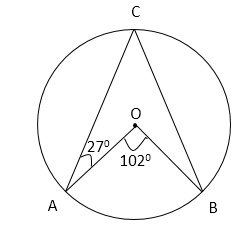
∠ACB = ½ x 1020 [Angle subtended by an arc at the centre is double the angle subtended by the arc at any point on the circle.]
=>∠ACB = 510
Reflex ∠AOB = 3600 – 1020 = 2580
∠OBC = 3600 – 270 – 2580 – 510 [Angle sum property of a quadrilateral]
=>∠OBC = 240
Quantity II: Find the value of ∠DBC.
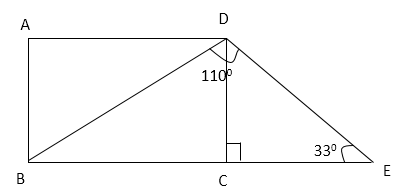
∠CDE = 1800 – 900 – 330 [Angle sum property of a triangle]
=>∠CDE = 570
Now, ∠CDB = 1100 – 570 = 530
∠DBC = 1800 – 900 – 530 [Angle sum property of a triangle]
=>∠DBC = 1800 – 1430
=>∠DBC = 370
Hence, Quantity I < Quantity II
9) Answer: a)
Quantity I:
Ratio of share in the profit:
Ajay: Subho: Jawed = (45000 x 8 + 90000 x 4) : (75000 x 12) : (60000 x 10)
= (360000 + 360000) : 900000 : 600000
= 720000 : 900000 : 600000
= 12:15:10
Share of Subho in the profit = 15/(12 + 15 + 10) x 222000
= 15/37 x 222000
= Rs.90000
Quantity II:
Let the share of Preeti, Amitabh and Suman be Rs.8x, Rs.6x and Rs.7x respectively.
Ratio of share in the profit:
Preeti : Amitabh : Suman = (8x + 8x + 4x) : (6x + 9x + 9x) : (7x + 7x + 7x)
= 20x : 24x : 21x
= 20:24:21
Share of Suman in the profit = 21/(20 + 24 + 21) x 325000
= 21/65 x 325000
= Rs.105000
Hence, Quantity I < Quantity II
10) Answer: a)
Quantity I:
Quantity of mixture in the first gallon = 7/(7 + 5) x 108
= 7/12 x 108
= 63 litres
Quantity of milk in the first gallon = 5/(5 + 4) x 63 = 35 litres
Quantity of water in the first gallon = 4/(5 + 4) x 63 + 10 = 28 + 10 = 38 litres
Quantity of mixture in the second gallon = 5/(7 + 5) x 108
= 5/12 x 108
= 45 litres
Quantity of milk in the second gallon = 5/(5 + 4) x 45 = 25 litres
Quantity of water in the second gallon = 4/(5 + 4) x 45 + 5 = 20 + 5 = 25 litres
Required difference = 38 – 25 = 13 litres
Quantity II:
Quantity of wine in the initial mixture = 3/(3 + 1) x 72
= ¾ x 72
= 54 litres
Quantity of water in the initial mixture = 1/(3 + 1) x 72
= 18 litres
Quantity of wine in the final mixture = 54 + 10 + ½ x 36
= 64 + 18
= 82 litres
Quantity of water in the final mixture = 18 + 8 + ½ x 36
= 44 litres
Required difference = 82 – 44 = 38 litres
Hence, Quantity I < Quantity II





