Dear Aspirants, the most awaited notification of SBI PO – 2019 has been released. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 6610]
Click Here to Take Free Mock Test For SBI PO Mains
Directions (Q. 1 – 5) Study the following information carefully and answer the given questions.
The following table shows the number of 4 different color balls in 6 different bags.
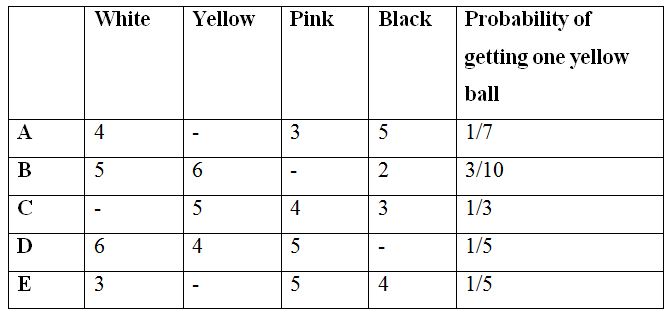
1) If 3 balls are taken out randomly from bag A, then find the probability of getting at least one pink ball from bag A?
a) 247/425
b) 78/217
c) 199/364
d) 123/289
e) None of these
2) If 4 balls are taken out randomly from bag C, then find the probability of getting different color balls from bag C?
a) 12/91
b) 45/77
c) 33/125
d) 127/245
e) None of these
3) If 4 balls are taken out randomly from bag D, then find the probability of getting 2 pink balls from bag D?
a) 56/121
b) 123/285
c) 92/157
d) 70/323
e) None of these
4) Find the ratio between the total number of balls in bag B to that of bag E?
a) 5 : 6
b) 4 : 3
c) 7 : 8
d) 5 : 4
e) None of these
5) Total number of pink balls in all the bags together is what percentage of total number of yellow balls in all the bags together?
a) 120 %
b) 80 %
c) 150 %
d) 100 %
e) 90 %
Directions (Q. 6 – 10) Study the following information carefully and answer the given questions:
The following table shows the number of working days of various companies in 6 different years.
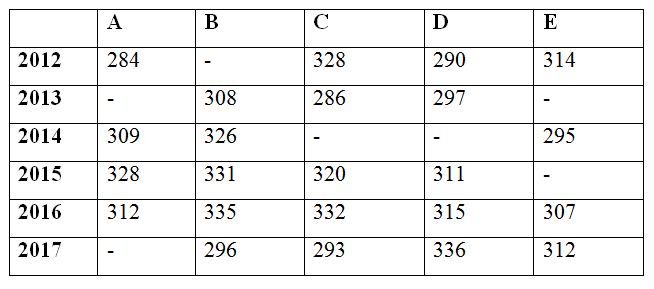
6) Find the difference between the number of working days of all the given companies in the year 2012 to that of 2015, if the average working days of company B in the year 2012 and 2013 is 310 days and the number of working days of company E in the year 2015 is 17 days less than the previous year?
a) 40 days
b) 20 days
c) 60 days
d) 80 days
e) None of these
7) Find the average number working days of all the given companies in the year 2014, if the ratio between the number of working days of C to that of D is 63 : 61 and the number of working days of C in the year 2014 is 5 less than that of the number of working days of C in the year 2015?
a) 325 days
b) 294 days
c) 288 days
d) 310 days
e) None of these
8) The number of working days of all the given companies in the year 2016 is approximately what percentage of the number of working days of all the given companies in the year 2017, if the ratio of number of working days of company D in the year 2013 to that of company A in the year 2017 is 9 : 10?
a) 125 %
b) 88 %
c) 102 %
d) 116 %
e) 134 %
9) Find the ratio between the number of working days of company D in the year 2014 to that of the company E in the year 2013, if the average number of working days of company D in all the given years together is 309 days and the total number of working days of company B and E in the year 2013 is 628 days?
a) 61 : 64
b) 55 : 57
c) 43 : 49
d) 22 : 25
e) None of these
10) The number of working days of company A and C in the year 2015 is approximately what percentage more/less than the number of working days of company B and E in the year 2017?
a) 20 % less
b) 7 % more
c) 20 % more
d) 7 % less
e) 30 % more
Answers :
Direction (1-5) :
1) Answer: c)
Let the yellow ball be x,
Probability of getting one yellow ball = 1/7
xC1/(12 + x)C1 = 1/7
x/(12 + x) = 1/7
7x = 12 + x
6x = 12
x = 2
Yellow balls in bag A = 2 balls
Total probability = 14C3
The probability of getting at least one pink ball
= > 1 – P(none is pink ball)
Probability of getting none is pink ball
= >11C3 /14C3 = 165/364
The probability of getting at least one pink ball
= > 1 – (165/364) = 199/364
2) Answer: a)
Let the white ball be X,
Probability of getting one yellow ball = 1/3
5C1/(12 + X)C1 = 1/3
5/(12 + X) = 1/3
15 = 12 + X
X = 3
The total white balls in bag C = 3
Total probability = 15C4
Required probability = 3C1 and 5C1 and 4C1 and 3C1
The probability of getting different color balls
= > [3C1 and 5C1 and 4C1 and 3C1]/15C4
= > 12/91
3) Answer: d)
Let the black ball be X,
Probability of getting one yellow ball = 1/5
4C1/(15 + X)C1 = 1/5
4/(15 + X) = 1/5
20 = 15 + X
X = 5
Total number of black balls = 5
Total probability = 20C4
Required probability = 5C2 and 15C2
The probability of getting 2 pink balls from bag D
= > (5C2 and 15C2)/20C4
= > 70/323
4) Answer: b)
Let the pink ball in bag B be X,
Probability of getting one yellow ball = 3/10
6C1/(13 + X)C1 = 3/10
6/(13 + X) = 3/10
13 + X = 20
X = 7
The total number of pink ball in bag B = 7 balls
Total balls in bag B = 5 + 6 + 7 + 2 = 20
Let the yellow ball in bag E be Y,
Probability of getting one yellow ball = 1/5
YC1/(12 + Y)C1 = 1/5
Y/(12 + Y) = 1/5
5Y = 12 + Y
4Y = 12
Y = 3
The total number of yellow ball in bag E = 3 balls
Total balls in bag E = 3 + 3 + 5 + 4 = 15
Required ratio = 20 : 15 = 4 : 3
5) Answer: a)
Let the pink ball in bag B be X,
Probability of getting one yellow ball = 3/10
6C1/(13 + X)C1 = 3/10
6/(13 + X) = 3/10
13 + X = 20
X = 7
The total number of pink ball in bag B = 7 balls
Total number of pink balls in all the bags together
= > 3 + 7 + 4 + 5 + 5 = 24
Let the yellow ball in bag A be Y,
Probability of getting one yellow ball = 1/7
YC1/(12 + Y)C1 = 1/7
Y/(12 + Y) = 1/7
7Y = 12 + Y
6Y = 12
Y = 2
Yellow balls in bag A = 2 balls
Let the yellow ball in bag E be Z,
Probability of getting one yellow ball = 1/5
ZC1/(12 +Z)C1 = 1/5
Z/(12 + Z) = 1/5
5Z = 12 + Z
4Z = 12
Z = 3
The total number of yellow ball in bag E = 3 balls
Total number of yellow balls in all the bags together
= > 2 + 6 + 5 + 4 + 3 = 20
Required % = (24/20)*100 = 120 %
Direction (6-10) :
6) Answer: a)
The average working days of company B in the year 2012 and 2013 = 310 days
The total working days of company B in the year 2012 and 2013
= > 310*2 = 620 days
The number of working days of company B in the year 2012 = 620 – 308 = 312
The number of working days of company E in the year 2015
= > The number of working days of company E in the year 2014 – 17
= > 295 – 17 = 278 days
The number of working days of all the given companies in the year 2012
= > 284 + 312 + 328 + 290 + 314 = 1528
The number of working days of all the given companies in the year 2015
= > 328 + 331 + 320 + 311 + 278 = 1568
Required difference = 1568 – 1528 = 40 days
7) Answer: d)
The ratio between the number of working days of C to that of D in the year 2014 = 63 : 61
The number of working days of C in the year 2014
= > The number of working days of C in the year 2015 – 5
= > 320 – 5 = 315
63’s = 315
1’s = 5
The number of working days of D in the year 2014 = 61’s = 61*5 = 305 days
Required average = (309 + 326 + 315 + 305 + 295)/5 = 1550/5 = 310 days
9) Answer: c)
The ratio of number of working days of company D in the year 2013 to that of company A in the year 2017 = 9 : 10
9’s = 297
1’s = 33
The number of working days of company A in the year 2017 = 10’s = 330 days
The number of working days of all the given companies in the year 2016
= > 312 + 335 + 332 + 315 + 307 = 1601
The number of working days of all the given companies in the year 2017
=> 330 + 296 + 293 + 336 + 312 = 1567
Required % = (1601/1567)*100 = 102 %
10) Answer: a)
The average number of working days of company D in all the given years together = 309 days
The total number of working days of company D in all the given years together = 309*6 = 1854
The number of working days of company D in the year 2014
= > 1854 – (290 + 297 + 311 + 315 + 336)
= > 1854 – 1549 = 305 days
The total number of working days of company B and E in the year 2013 = 628
The number of working days of company E in the year 2013
= > 628 – 308 = 320 days
Required ratio = 305 : 320 = 61 : 64
10) Answer: b)
The number of working days of company A and C in the year 2015
= > 328 + 320 = 648 days
The number of working days of company B and E in the year 2017
= > 296 + 312 = 608 days
Required % = [(648 – 608)/608]*100 = 7 % more





