Simplification Problems PDF: Practice Questions with Tricks for Bank & Other Exams

By admin - Nov 16 2022

Simplification basics and tricks are available here. For all competitive exams, candidates can use these Most Important Simplification questions with answers for practice. Tricks given here will be helpful to solve the questions very quickly and score good marks. Simplification sums are the most expected topics in all Competitive exams in the quantitative aptitude section and it is one of the Important Topics which help to Increase Your Score. So, practice more simplification questions for bank exam and other competitive exams. The simplification for bank PO exams will be slightly tricky and time-consuming. So, take more Simplification questions with answers and boost your overall score. Also, take more Simplification quiz practice by which you can gain the ability to solve the questions quickly. Below we have given the List of Most Expected Types of Simplification Questions for bank exam along with answers.

What is Simplification?

Mathematics is a Complex Web. If you want to know the answer to How do I make this conclusion? Read this article then it will be so simple. Simplification will be an important topic on all competitive exams like SBI PO, SBI Clerk, IBPS PO, IBPS Clerk, SSC CGL, SSC CHSL, and others. Simplification means finding the solution from the complex calculation. So understanding the significance of simplification will enhance your overall mental power. In this article, you can get Tricks of Simplification, Techniques, and more questions to practice for Simplification.

Simplification Questions for bank exam

Simplification questions for bank exam come under quantitative aptitude. Bank exams like IBPS Clerk, IBPS PO, and SBI will focus on quantitative aptitude because banks require a lot of quantitative aptitude skills for their performance. So Aspirants should focus on Simplication Questions for bank exam. For that they should know why Simplification skills are required for banking. To know about that Aspirants should read our article completely.

Types of Simplification Sums:

There are two possible ways to ask a question that is related to simplification. Simplification questions will take place in all important competitive exams because we can check individual analytical thinking through simplification.

  • Finding the missing number from the calculation will be the first type of simplification. In this type to get a solution to approximate the given number or we can simplify using the basic operations.
  • The second method will understand the relation between the numbers and simplify the numbers using the rules of simplification.

Try Simplification Free Online Mock Test

Examples with an explanation for Simplification Questions for bank exam with answers:

1). (10.8×16×12)  + (3.6×56×9.2)   =?

  1. 3941.35
  2. 3966.89
  3. 3928.32
  4. 3649.19
  5. 3645.19
Ans: c
Solution:
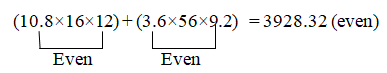
Simplification problems
Even + Even should be always Even. So the unit digit should be in even.
Note: All numbers should be Even.
2). 12.3% of 203 + 23% of  1110 =?
  1. 270.269
  2. 240.269
  3. 280.269
  4. 290.269
  5. None of these
Ans :c
Solution:
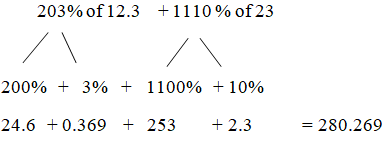
Simplification pdf
Simplification Tricks :      A% of B = B % of A
  1. 3/4
  2. 5/7
  3. 3/7
  4. 4/7
  5. None of these

Ans: b
Solution:
Simplification Tricks:

4). 3545 ×14.75 – 2325 ×15.25 =?

  1. 15369.5
  2. 16832.5
  3. 11546.5
  4. 12475.5
  5. None of these

Ans: b
Solution:
1220×15 – 5870 ×0.25 = 16832.5
(15+0.25=15.25; 15-0.25=14.75) (a-b , a+b)
Here,
3545+2325=5870 (x+y)
3545– 2325 =1220 (x-y)

5). 27% of 250 +22% of 920 +21% of 660=?

  1. 419.5
  2. 423.5
  3. 408.5
  4. 415.5
  5. None of these

Ans: c
Solution:
Common percentage method:
(250+920+660) =1830
Here 20% is common;
20% of 1830 =366
Further,
1st part (20+7) = 7% of 250 =17.5
2nd part (20+2) = 2% of 920 =18.4
3rd part (20+1) = 1% 660 = 6.6
366+17.5+18.4+6.6 = 408.5

6). 212 +172 -132 = ?

  1. 412
  2. 512
  3. 561
  4. 461
  5. None of these

Ans: c
Solution:
Method:
212 +(172 -132) = 212 +((17+13)(17-13)) = 441 +(30×4) =561
Note: (A2 – B2) = (a+b) (a-b)

7). (22×28)  +  (38×42) = ?

  1. 2122
  2. 2212
  3. 2132
  4. 2213
  5. None of these

Ans: B
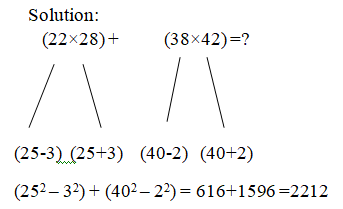
simplification
Simplification Tricks:  If any two numbers in multiplication with the common base number, we can use this method

8). 12.75% of 464 =?

  1. 59.96
  2. 57.16
  3. 51.86
  4. 59.16
  5. None of these

Ans: D
Solution:
(12.75×4) of (464/4) = 51% of 116 =59.16
Simplification Tricks: If any fractional number ends with 5, we can convert that into a whole number by this method.

9). 8.2% of 780 +x= 12.9% of 1310

  1. 107.26
  2. 106.53
  3. 105.03
  4. 103.56
  5. None of these

Ans: c
Solution:
82×78/100 + X =129×131 /100
(130-1)(130+1) /100 – (80+2)(80-2) /100 =X
X=105.03
10). 0.875 of 848  + 0.625 of 624= ?

  1. 1132
  2. 1325
  3. 1236
  4. 1250
  5. None of these

Ans: A
Solution:
87.5% of 848 + 62.5% of 624
(7/8 ×848) +  5/8 ×624 = 742 +390 =1132
Simplification Tricks: 87.5% = (100-12.5)%
                      = (1-1/8) =7/8

Simplification Tricks and Techniques:

            Simplification -large, complex numerical expression into a simpler form by performing various mathematical operations, in accordance with the BODMAS rule.
B  àStands for bracket and operation of brackets in the order ( ),( ),{ }and[ ]
OàStands for ‘of ‘(usage is x)
DàStands for division (/)
MàStands for multiplication (x)
A à Stands for addition (+)
S à Stands for subtraction (-)

Try Topic Wise Online Mock Test

Simplification Tricks –Easiest way to choose simplification questions for bank exam:

STEP 1: Know about BODMAS Rule. Following are the list of priority given for brackets and signs.
STEP 2: If an expression Contains brackets, the expression within the brackets should be simplified first.
STEP 3: If an expression contains ‘Of’, multiplication, division, addition, and subtraction, then of should be performed first then followed by multiplication or division.
Proceeding from left to right, addition, and subtraction are carried out in the order in which the sign of addition and subtraction are given.
If an expression contains ‘Of’ and Division – always do ‘Of’ and then do division
STEP 4: If expression involves all four operations, then multiplication and division are carried out first in the order in which they are given from left to right. The same rules are carried out for addition and subtraction.

Learn squares and cubes of number (Simplification Tricks)

Simplification Tricks – Squares(12 to 302):

·        12 – 1
·        22 – 4
·        32 – 9
·        42 – 16
·        52 – 25
·        62 – 36
·        72– 49
·        82 – 64
·        92– 81
·        102-100
·        112 -121
·        122-144
·        132 – 169
·        142– 196
·        152 – 225
·        162– 256
·        172 – 289
·        182– 324
·        192 – 361
·        202 – 400
·        212 – 441
·        222– 484
·        232 – 529
·        242– 576
·        252 – 625
·        262 – 676
·        272 – 729
·        282 – 784
·        292 – 841
·        302 – 900

 Simplification Tricks – Cubes (13to 153):

·        13 – 1
·        23– 8
·        33 – 27
·        43 – 64
·        53 – 125
·        63 – 216
·        73 – 343
·        83 – 512
·        93 – 729
·        103 – 1000
·        113 – 1331
·        123 – 1728
·        133 – 2197
·        143 – 2744
·        153 – 3375

Example 1: 212 / 49 × 6

Solution: From the above question if we know the square value of 212, then this question will be easily solved
STEP 1:212= 441
STEP 2:441/49= 9
STEP 3:9×6 = 54
STEP 4:Hence the answer for the above series is 54

REMEMBER FREQUENTLY ASKED FRACTION VALUES (Simplification Tricks)

·        5% = 0.05
·        6 ¼ % = 0.0625
·        10% = 0.1
·        12 ½ = 0.125
·        16 × (2/3)% = 0.166
·        20 % = 0.2
·        25 % = 0.25
·        33 × (1/3)%= 0.33
·        40 % = 0.4
·        50% = 0.5
·        60% = 0.6
·        66 × (2/3) =0.66
·        75 %= 0.75
·        80 %= 0.8
·        90 % = 0.9
·        100% = 1
·        125 % = 1.25
·        150% = 1.5
·        200 % = 2
·        250 % =2.5
Example 2): 60% of 250 +25% of 600
STEP 1: Know the values of 60% =0.6 and 25 % = 0.25
STEP 2: Now directly multiply 0.6×250 + 0.25×600
STEP 3:0.6×250= 150
            0.25×600=150
STEP 4: 150+ 150 = 300
STEP 5:Hence the answer for the above series is 300
 
Example 3): Solve mixed fraction – Multiplication
EXAMPLE 3: 2×(3/5) × 8×(1/3) + 7 ½ × 2×(2/3)
STEP 1:2×(3/5) × 8×(1/3) = (13/5) × (25/3) = 65/3
STEP 2:  + 7 ½ ×2×(2/3)= 43/6 × 12/5 = 86/5
STEP 3:65/3 + 86/5 = 38×(15/13)
STEP 4:hence the answer for the above series is38×(15/13)
Example 4): Solve Mixed Fraction addition
Example 4:19×(3/5) + 23×(2/3) – 24×(1/5)
STEP 1:Take all the whole number outside the bracket i.e. 19+23 -24 = 18
STEP 2:Add fractions within bracket 18×[(3/5) + (2/3) – (1/5)] = 18(16/15)
STEP 3:  Hence the answer for the above series is18(16/15)
 
Example 5): (?)2+18×12= 62×5×2
STEP 1:Multiply 18 × 12 = 216
STEP 2:Square of 6 = 36
STEP 3:Multiply 36 ×5×2= 360
STEP 4:(X)2 +216 = 360
STEP 5:(X)2  = 360-216 = 144
STEP 6:Therefore X = 12

Download Simplification Example Problems for Bank Exams PDF

Get All Section Study Materials

43 responses to “Simplification Problems PDF: Practice Questions with Tricks for Bank & Other Exams”

  1. yandex.ru says:
    August 19, 2026 at 4:26 pm

    Обязательный диагностика представляет собой обязательной мерой для поддержания надёжности транспортного средства.
    Во время проверки обнаруживаются скрытые неисправности, которые могут вызвать серьёзных поломок на трассе.
    Своевременное прохождение ТО помогает избежать больших вложений на сложный ремонт позже.
    Кроме того исправный автомобиль гарантирует спокойствие вашу и окружающих на пути.
    https://yandex.ru/maps/org/tekhosmotr/11324347330

    Reply
  2. NathanDrill says:
    August 18, 2026 at 3:08 pm

    На этой платформе удастся обнаружить реестр достоверной данных.
    В этом каталоге приведены номера предприятий и ИП.
    Указанная информация представляют собой общедоступными и способны применены для уточнения контактов.
    Ресурс регулярно актуализируется, дабы пользователь в любой момент имели свежей информацией.
    https://orq.me/

    Reply
  3. NathanDrill says:
    August 17, 2026 at 3:18 pm

    На этой платформе вы сможете получить доступ реестр достоверной данных.
    В этом каталоге приведены контакты учреждений и индивидуальных предпринимателей.
    Указанная информация считаются открытыми и могут быть востребованы в целях поиска реквизитов.
    Портал регулярно актуализируется, чтобы пользователь всегда располагали актуальной базой.
    https://orq.me/

    Reply
  4. Jerrytrank says:
    August 17, 2026 at 1:24 am

    Mindful gaming is an approach that supports users to retain control over their gambling engagement while understanding the likely pitfalls.
    https://www.soundclick.com/IvanBabak

    Reply
  5. Jerrytrank says:
    August 16, 2026 at 7:13 pm

    Mindful gaming is a methodology that facilitates players to maintain management over their wagering activity while understanding the inherent risks.
    https://peatix.com/user/30026556/view

    Reply
  6. Jerrytrank says:
    August 16, 2026 at 12:29 pm

    Mindful gaming is an approach that ensures players to preserve discipline over their gambling decisions while identifying the possible harms.
    https://goszakaz-udm.ru/novosti/2026-07-28-sekrety-uspeshnogo-strimera-igrayushchego-v-desertnye-sloty-kontent-auditoriya-monetizatsiya/

    Reply
  7. Laskica says:
    August 16, 2026 at 8:56 am

    На этом сайте вы сможете обнаружить массу ценной материалов.
    https://bestadsontv.com/profile/525269/Angelina-Morozova

    Reply
  8. Jerrytrank says:
    August 16, 2026 at 6:07 am

    Prudent betting is a methodology that encourages players to keep discipline over their betting activity while identifying the potential risks.
    https://reactormag.com/members/ivanbabak2026/profile

    Reply
  9. Jerrytrank says:
    August 15, 2026 at 11:15 pm

    Responsible gambling is a set of principles that ensures players to maintain mastery over their wagering decisions while identifying the possible harms.
    https://billiard-house.ru/blog/2385-trekhdnevnaya-rabochaya-nedelya-pered-novym-godom-initsiativa-senatora-gibatdinova.html

    Reply
  10. Laskica says:
    August 15, 2026 at 7:07 pm

    Interactive entertainment give gamers the enjoyable means to connect and play with friends everywhere.
    https://animallover.mixwatch.ru/0p6o6yUzXgWD/

    Reply
  11. Jerrytrank says:
    August 15, 2026 at 4:27 pm

    Responsible gambling is a framework that supports players to retain discipline over their playing activity while noticing the likely pitfalls.
    https://zhkhtv.ru/read-full/940-belgrad-gorel-vsyu-noch-protesty-prevratilis-v-polnotsennuyu-ulichnuyu-voynu.html

    Reply
  12. Jerrytrank says:
    August 15, 2026 at 9:28 am

    Responsible gambling is a practice that encourages users to sustain control over their playing engagement while identifying the inherent risks.
    https://www.trustami.com/review/6a74a4b3e218a2001c50cb6f-rating

    Reply
  13. Jerrytrank says:
    August 14, 2026 at 9:27 pm

    Controlled play is an approach that encourages participants to preserve management over their gaming engagement while acknowledging the potential risks.
    https://www.soundclick.com/IvanRogov

    Reply
  14. Jerrytrank says:
    August 14, 2026 at 2:51 pm

    Safe wagering is a practice that ensures participants to exercise mastery over their playing behaviour while noticing the inherent risks.
    https://sretenkadesignweek.ru/look/101-mobilnye-sloty-kak-optimizirovat-igrovoy-opyt-na-smartfonakh-i-planshetakh/

    Reply
  15. Jerrytrank says:
    August 14, 2026 at 4:34 am

    Mindful gaming is a set of principles that encourages participants to retain mastery over their playing decisions while recognising the attendant dangers.
    https://parket-danichgroup.ru/

    Reply
  16. Jerrytrank says:
    August 13, 2026 at 10:12 pm

    Responsible gambling is a framework that supports participants to preserve discipline over their gaming engagement while noticing the inherent risks.
    https://projects.blender.org/Ivan-Dolin

    Reply
  17. Jerrytrank says:
    August 13, 2026 at 3:32 pm

    Mindful gaming is an approach that facilitates players to exercise management over their gaming actions while recognising the likely pitfalls.
    https://studiogp.ru/

    Reply
  18. Laskica says:
    August 13, 2026 at 12:33 am

    На этом сайте вы сможете найти интересную информацию.
    https://balmain1.ru/

    Reply
  19. 🏛️ You have A NEW MESSAGE #J1485 OPEN => linkspree.net/p/you-have-1-new-message-0637af?hs=95b50165c04d5394170349e01ee3049f& 🏛️ says:
    August 12, 2026 at 3:41 pm

    sktpwg

    Reply
  20. Laskica says:
    August 11, 2026 at 7:38 pm

    Здесь сайте удастся отыскать нужную информацию.
    https://nbcollector.ru/

    Reply
  21. azeri gay xxx says:
    August 11, 2026 at 7:16 am

    Аббревиатура ЛГБТ охватывает людей с различной сексуальностью и разнообразием гендерных идентичностей gay anime xxx gif

    Reply
  22. Laskica says:
    August 4, 2026 at 10:10 pm

    На этом сайте удастся отыскать интересную информацию.
    https://lepodium.net/

    Reply
  23. Ранд Экс бонусы says:
    August 1, 2026 at 12:12 am

    Контролируемый игровой процесс — это подход, предназначенный на обеспечение дисциплины над игровым поведением и понимание рисков, связанных с азартными играми, при одновременном акценте на досуг как основную функцию участия.
    https://randx-super.ru/

    Reply
  24. Ранд Экс промокод says:
    July 30, 2026 at 1:57 am

    Безопасное увлечение ставками — это подход, ориентированный на поддержание контроля над своими решениями и признание рисков, связанных с азартными играми, при параллельном акценте на отдых как базовую цель участия.
    https://randx-super.ru/

    Reply
  25. randx-super.ru says:
    July 30, 2026 at 12:55 am

    Безопасное увлечение ставками — это метод, предназначенный на обеспечение дисциплины над финансовыми расходами и осознание потенциальных проблем, связанных с участием в ставках, при параллельном упоминании на досуг как основную функцию участия.
    https://randx-super.ru/

    Reply
  26. 📈 Top Up 236,538 $. GET ->> graph.org/BALANCE-3682444-USD-04-21-2?hs=95b50165c04d5394170349e01ee3049f& 📈 says:
    July 29, 2026 at 7:03 am

    dlpt3d

    Reply
  27. Jerrytrank says:
    July 27, 2026 at 3:55 am

    Conscious gaming is a system that encourages users to preserve oversight over their playing decisions while acknowledging the possible harms.
    https://n1.mvmedia.ru/ZHlQRqxoY1X5/

    Reply
  28. Jerrytrank says:
    July 27, 2026 at 3:01 am

    Controlled play is a system that promotes players to maintain discipline over their wagering habits while understanding the possible harms.
    https://fashionista.femalemoda.ru/EkrJcoJMbPhh/

    Reply
  29. mcqquestions.net says:
    July 20, 2023 at 8:18 pm

    Aptitude questions and answers for student to practice previous year exams, interview, competitive examination and entrance exams

    Reply
  30. Srishti Purohit says:
    June 6, 2021 at 1:13 pm

    This helped me alot…thankyou

    Reply
  31. hans raj singh says:
    January 19, 2018 at 8:57 pm

    10.8*16*12+3.6*56*9.2 please explain sir full

    Reply
  32. hans raj singh says:
    January 19, 2018 at 8:56 pm

    10.8*16*12+3.6*56*9.2 please explean sir

    Reply
  33. SANDEEP KAUR says:
    December 29, 2017 at 9:24 am

    thank u sir

    Reply
  34. jyo says:
    December 9, 2017 at 6:15 am

    thanq sir

    Reply
  35. Tapan says:
    December 8, 2017 at 10:50 pm

    ohh very nice

    Reply
  36. Tapan says:
    September 14, 2017 at 9:03 pm

    sir 1-30 squire is enough? one math teacher say one candidate must memorize sqire up to 150 and cube up to 50.

    Reply
  37. Srinivasan Myfamliy says:
    September 14, 2017 at 10:55 am

    tanq@@

    Reply
  38. BAHUBALI says:
    September 14, 2017 at 9:09 am

    thanks ig qube of 14 is wrong correct it..

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

© 2026 All rights reserved. Made with by IBPSGuide