SSC CGL EXAMS 2018 | Quantitative Aptitude Practice Questions (Day-20)

Dear Aspirants, Here we have given the Important SSC Exam 2018 Practice Test Papers. Candidates those who are preparing for SSC 2018 can practice these questions to get more confidence to Crack SSC 2018 Examination.

[WpProQuiz 4849]

Click Here for SSC CGL Online Mock Test 

 Click here to view Quantitative Aptitude Questions in Hindi

1)  ABCD is a trapezium, such that AB, DC is parallel and BC is perpendicular to them. If 

a) 6 cm

b) 4 cm

c) 3 cm

d) 5 cm

2) A conical tent of given capacity has to be constructed. The ratio of the height to the radius of the base for the minimum amount of canvas required for the tent is:

a) 1: 2

b) 1 : √2

c) 2 : 1

d) √2 : 1

3) If a group of children each boy gave a gift to each other. If total 10302 gifts were distributed, then find the number of boys?

a) 102

b) 104

c) 101

d) 170

4) Find the volume of the metal of a hollow spherical shell whose thickness is 0.01 in and internal radius is 5 in

a) 2π

b) 3 π

c) 4 π

d) π/3

5) On a particular day of a trade fair, 35,000 visitors had visited the fair. The amount collected at the entrance counter was Rs. 9, 50,000. The entrance fee was at the rate of Rs. 20 for a child. If 10% of the visitors had used free passes, the number of children who visited the fair is

a) 15,500

b) 31,500

c) 12,500

d) 16,000

6) If A is Arithmetic mean (AM) and H is Harmonic Mean (HM) between two quantities a and b, then,   will be equal to

a) A/H

b) H/A

c) A+H/A – H

d) a – b/ A – H

7) The price of diamond is proportional to the square of its weight. If the price of a diamond weighing 5 carats is Rs.225, then find the price of another diamond weighing 9 carats.

a) 929

b) 729

c) 125

d) 624

8) PQRS is a square whose side is 44 cm each, taking PQ and PS as axes, the equation of the circle circumscribing the square is

a) x² + y² = 22(x + y)

b) x² + y² = 11 (x + y)

c) x² + y² = 44 (x + y)

d) x² + y² = 4(x + y)

9) What is the remainder of  7³⁸⁹²/13 ?

a) 0

b) 1

c) 2

d) 7

10) If LCM of two natural number x and y is 1440 then how many such pairs exist?

a) 80

b) 83

c) 60

d) 165

Answers :

1) Answer: d)

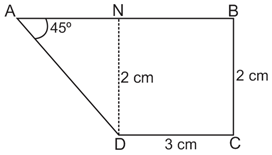
Tan 45⁰ = DN/AN

1 = DN/AN

AN = DN = 2 cm

AB = AN + BN

AB = 2 + 3 = 5 cm

2) Answer:  d)

Curved surface area of cone = πrl

l = √(h² + r²)

After substituting the value given in options to get two answer

∴ The lease value is √3π, when h = √2 and r = 1

3) Answer: a)

Let number of boys = x

Number of gifts given = x – 1

X (x – 1) = 10302

X² – x – 10302 = 0

Solving this equation

(x – 102)(x + 101) = 0

X = 102

4) Answer:  d)

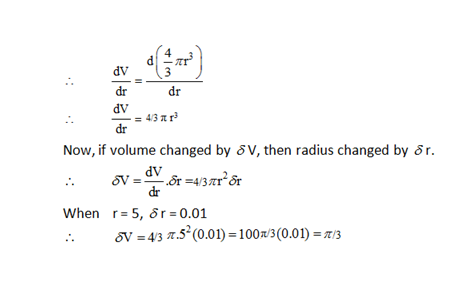
5) Answer: a)

Total number of visitors on a particular day of the trade fair = 35000

The number of visitors who paid the entrance fee = 90% of 35000

= (90/100) * 35000 = 31500

Now, let the number of children who visited the fair be x.

40 (31500 – x) + 20x = 950000

1260000 – 40x + 20x = 950000

1260000 – 20x = 950000

20x = 310000

x = 15500

6) Answer:  a)

Given, A =(a+b)/2

H = 2ab/ (a+b)

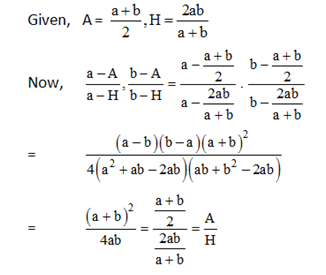
7) Answer: b)

Price of Diamond = Weight²

According to the question, 5²/ 9² = 225/x

X = (9 * 9 * 225) / (5 * 5) = 729

8) Answer: c)

Center of circle = (22, 22)

By general equation of circle

x² + y² — 44x – 44y = 0

x² + y² = 44 (x + y)

9) Answer: b)

Here we have divisor as 13 and we have to find the Euler’s Totient of 13.

13 (d) = 13 × 1 – 1/13 = 12, Here 7 is co-prime to 13 hence we can apply Euler’s theorem, From Euler’s theorem remainder of  has remainder 1.

10) Answer: b)

1440 = 2 × 720

= 2 × 2 × 2 × 2 × 2  × 3 × 3 × 5

= 2⁵ × 3² × 5¹

Then numbers of such pairs are—

*******************

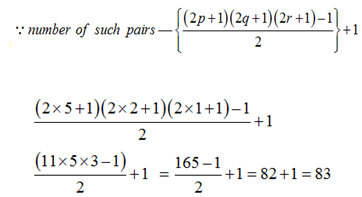
Click Here for SSC CGL Online Mock Test 

Click Here for More Quizzes

SSC CGL EXAMS 2018 |Quantitative Aptitude Practice Questions (Day-19) 

SSC CGL EXAMS 2018 |Quantitative Aptitude Practice Questions (Day-18) 

SSC CGL EXAMS 2018 |Quantitative Aptitude Practice Questions (Day-17)