Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4708]Click Here for IBPS Clerk Mains Online Mock Test
Click here to View Quantitative Aptitude Questions in Hindi
Direction (1 – 5): Read the following information carefully and answer the given questions:
In one of the village have five different schools. The number of boys in school A is one-eighth of the total students. The number of boys in school B is 10% of the total students in all the five schools together. The ratio between the numbers of girls to boys in school E is 1:1. The number of boys in school A is equal to the sum of number of boys in school B and the number of boys in school E. The number of girls in school C is 20% of the total number of girls. The number of boys in school C is three-two of the number of boys in school B. The number of students in school A is 50% more than the number of students in school D. The number of students in school B is 15% of the total students. The total boy in all the five schools together is 200 less than the total number of girls in all the five schools together. The total number of students in all the five schools together is 1200.
1) What is the difference between the total number students in which school has the highest number of girls and the total number of students in which school has the highest number of boys?
a) 64
b) 72
c) 68
d) 78
e) None of these
2) From a group of number of boys in school D and the number of girls in school E, two students are selected at random. Find the probability that at least one girl is selected?
a) 207/245
b) 183/245
c) 121/2450
d) 99/245
e) None of these
3) What is the ratio of girls to boys in School F?
Statement I: Total number of boys in School F is 200% of the number of students in School E.
Statement II: Total number of girls in School F is 130 less than the total number of students in School F.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
4) Quantity I: What is the average number of boys in school A, E, C together?
Quantity II: What is the average number of girls in School B and D together?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
5) Quantity I: What is the difference between the total number of students in School A and B?
Quantity II: What is the difference between the total number of students in School D and E?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
Directions (6 – 10): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and answer the questions given below.
6)
I. 8, 4, 6, 15, 52.5
II. 12 …. 78.75. If 78.75 is the nth term, then find the value of n?
a) 6
b) 4
c) 5
d) 7
e) 8
7)
I. 29, 59, 178, 891, 6238
II. 46 ….. 9808. If 9808 is the nth term, then find the value of n?
a) 6
b) 5
c) 7
d) 8
e) 9
8)
I. 45, 92, 372, 2984, 47760
II. 2.5 ….. 135712. If 135712 is the nth term, then find the value of n?
a) 9
b) 8
c) 7
d) 6
e) 11
9)
I. 11, 12, 26, 108, 872, 13968
II. 4 …… 217632. If 217632 is the nth term, then what value should come in the place of (n-1)th term?
a) 5016
b) 4820
c) 2560
d) 4520
e) 6800
10)
I. 1024, 1267, 1348, 1510, 1564, 1672, 1708
II. 961 ….. 1717. If 1717 is nth term, then what value should come in the place of (n – 2)th term?
a) 1339
b) 1559
c) 1609
d) 1753
e) 1497
Answers:
Directions (1 – 5):
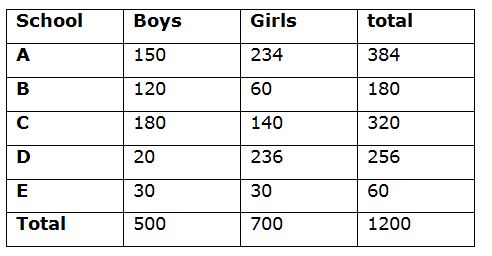
Total number of students=1200
Girls + Boys = 1200 —> (1)
Boys is 200 less than girls,
Girls – Boys = 200 —> (2)
So the number of boys =500
The number of girls=700
Number of Boys in school A = (1/8)*1200 = 150
Number of boys in school B = (10/100)*1200 = 120
Number of boys in school E = 150 – 120 = 30
Number of girls in school E = (1/1)*30 = 30
Total number of students in school E = 30+30 = 60
Number of boys in school C = (3/2)*120 = 180
Number of boys in school D = 500 – 150 – 120 – 30 – 180 = 20
Number of girls in school C = (20/100)*700 = 140
Total number of students in School C = 140 + 180 = 320
Total number of students in School B = (15/100)*1200 = 180
Number of girls in school B = 180 – 120 = 60
Number of students in A and D = 1200 – (180 + 320 + 60) = 640
Total number of students in School A=150/100 school D
D + (150/100)*D=640
D + (3/2)*D=640
5D = 640*2
Number of students in school D=256
Number of students in school A = 640 – 256 = 384
Number of girls in school A = 384 – 150 = 234
Number of girls in School D = 256 – 20 = 236
1) Answer: a)
Highest number of girls in school D, the total number students in school D=256
Highest number of boys in school C, the total number of students in school C=320
Required difference = 320 – 256 = 64
2) Answer: a)
Number of boys in school D=20
Number of girls in school E=30
50C2=50*49/1*2=1225
n(E)=20C1*30C1 + 30C2
=20*30+(30*29)/(1*2)
=600 + 435 =1035
Required probability = 1035/1225 = 207/245
3) Answer: e)
From statement I,
Number of boys in school F=60*(200/100)=120
So, Statement I alone is not sufficient to the answer the question.
From Statement II,
Total number of students in school F = x
Number of girls in School F = x – 130
So, statement II alone is not sufficient to the answer the question.
From I, II
X=120+x-130
So, both statement I and II are also not sufficient to the answer the question.
4) Answer: c)
From quantity I,
Average= (150+30+180)/3 = 120
From quantity II,
Average= (60+236)/2 = 148
Quantity II > Quantity I
5) Answer: a)
From quantity I,
Difference = 384 – 180 = 204
From quantity II,
Difference = 256 – 60 = 196
Quantity I > Quantity II
Directions (6-10):
6) Answer: c)
Series – I pattern:
8 is the 1st term
8 * 0.5 = 4
4 * 1.5 = 6
6 * 2.5 = 15
15 * 3.5 = 52.5
52.5 is the 5th term
Series – II pattern:
12 is the 1st term
12 * 0.5 = 6
6 * 1.5 = 9
9 * 2.5 = 22.5
22.5 * 3.5 = 78.75 = 5th term
7) Answer: b)
Series –I pattern:
29 is the 1st term
29 * 2 + 1 = 59
59 * 3 + 1 = 178
178 * 5 + 1 = 891
891 * 7 + 1 = 6238 = 5th term
Multiply with prime numbers and add 1 after multiplication
Series –II pattern:
46 is the 1st term
46 * 2 +1 = 93
93 * 3 + 1 = 280
280 * 5 + 1 = 1401
1401 * 7 + 1 = 9808 = 5th term
Multiply with prime numbers and add 1 after multiplication
8) Answer: d)
Series –I pattern:
45 is the 1st term
45 * 2 + 2 = 92
92 * 4 + 4 = 372
372 * 8 + 8 = 2984
2984 * 16 + 16 = 47760 = 5th term
Series – II pattern:
2.5 is the 1st term
2.5 * 2 + 2 = 7
7 * 4 + 4 = 32
32 * 8 + 8 = 264
264 * 16 + 16 = 4240
4240 * 32 + 32 = 135712 = 6th term
9) Answer: e)
Series – I pattern:
11 is the 1st term
11 * 20 + 20 = 12
12 * 21 + 21 = 26
26 * 22 + 22 = 108
108 * 23 + 23 = 872
872 * 24 + 24 = 13968 = 6th term
Series – II pattern:
4 is the 1st term
4 * 20 + 20 = 5
5 * 21 + 21 = 12
12 * 22 + 22 = 52
52 * 23 + 23 = 424
424 * 24 + 24 = 6800 = (7 – 1)th term
6800 * 25 +25 = 217632 = 7th term
10) Answer: c)
Series – I pattern:
1024 is the 1st term
1024 + 243 = 1267
1267 + (243/3) = 1348
1348 + (81*2) = 1510
1510 + (162/3) = 1564
1564 + (54*2) = 1672
1672 + (108/3) = 1708 = 7th term
Series – II pattern:
961 is the 1st term
961 + 243 = 1204
1204 + (243/3) = 1285
1285 + (81*2) = 1447
1447 + (162/3) = 1501
1501 + (54*2) = 1609 = (8-2)th term
1609 + (108/3) = 1645 = (8-1)th term
1645 + (36*2) = 1717 = 8th term
Click Here for IBPS Clerk Mains Online Mock Test
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| IBPS SO/NIACL AO Prelims – Reasoning | 10.00 AM |
| IBPS SO/NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| IBPS SO/NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





