Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for IBPS RRB PO Prelims 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
IBPS RRB PO Mains Free Mock Test 2019
[WpProQuiz 6568]
Directions (Q. 1 – 5): In the following questions, two equations I and II are given. You have to solve both the equations and give Answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
1)
I) 2x2 – 16x + 32 = 0
II) 3y2 – 15y + 18 = 0
2)
I) x2 – 4x – 77 = 0
II) y2 – 27y + 92 = 0
3)
I) 4x + 5y + 26 = 0
II) 3x – 4y + 4 = 0
4)
I) 3x2 + 14x + 15 = 0
II) 3y2 – 13y + 14 = 0
5)
I) 4x2 – 6x – 18 = 0
II) 5y2 + 6y – 27 = 0
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following table shows the total number of employees working in 5 different departments and the percentage of females among them.
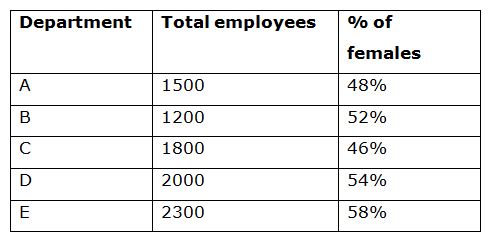
6) Find the ratio between the total number of males working in department A to that of total number of females working in department D?
a) 13 : 18
b) 27 : 35
c) 22 : 29
d) 11 : 15
e) None of these
7) Find the total number of unmarried males in department B and E together, if the ratio between the total number of married males to that of unmarried males is 19 : 13 and 2 : 1 respectively?
a) 584
b) 632
c) 678
d) 556
e) None of these
8) Find the average number of females working in department B, C and D together?
a) 812
b) 844
c) 878
d) 926
e) None of these
9) Total number of females working in department A and E together is approximately what percentage of total number of males working in department C and D together?
a) 109 %
b) 125 %
c) 142 %
d) 95 %
e) 156 %
10) Total number of employees working in department A and B together is approximately what percentage more than the total number of employees working in department E?
a) 6 %
b) 32 %
c) 17 %
d) 45 %
e) 58 %
Answers:
Directions (1-5):
1) Answer: a)
I) 2x2 – 16x + 32 = 0
2x2 – 8x – 8x + 32 = 0
2x (x – 4) – 8 (x – 4) = 0
(2x – 8) (x – 4) = 0
x = 8/2, 4 = 4, 4
II) 3y2 – 15y + 18 = 0
3y2 – 9y – 6y + 18 = 0
3y (y – 3) – 6 (y – 3) = 0
(3y – 6) (y – 3) = 0
y = 6/3, 3 = 2, 3
x > y
2) Answer: e)
I) x2 – 4x – 77 = 0
(x – 11) (x + 7) = 0
x = 11, -7
II) y2 – 27y + 92 = 0
(y – 23) (y – 4) = 0
y = 23, 4
Can’t be determined
3) Answer: c)
4x + 5y = – 26 –> (1)
3x – 4y = – 4 –> (2)
By solving the equation (1) and (2), we get,
x = -4, y = -2
x < y
4) Answer: c)
I) 3x2 + 14x + 15 = 0
3x2 + 9x + 5x + 15 = 0
3x (x + 3) + 5 (x + 3) = 0
(3x + 5) (x + 3) = 0
x = -5/3, -3
II) 3y2 – 13y + 14 = 0
3y2 – 6y – 7y + 14 = 0
3y (y – 2) – 7 (y – 2) = 0
(3y – 7) (y – 2) = 0
y = 7/3, 2
x < y
5) Answer: e)
I) 4x2 – 6x – 18 = 0
4x2 – 12x + 6x – 18 = 0
4x(x – 3) + 6(x – 3) = 0
(4x + 6) (x – 3) = 0
x = -6/4, 3 = -3/2, 3 = -1.5, 3
II) 5y2 + 6y – 27 = 0
5y2 + 15y – 9y – 27 = 0
5y(y + 3) – 9(y + 3) = 0
(5y – 9) (y + 3) = 0
y = 9/5, -3 = 1.8, -3
Can’t be determined
Directions (6-10):
6) Answer: a)
The total number of males working in department A
= > 1500 * (52/100)
The total number of females working in department D
= > 2000 * (54/100)
Required ratio = [1500 * (52/100)] : [2000 * (54/100)]
= > 13 : 18
7) Answer: d)
The total number of unmarried males in department B and E together
= > 1200 * (48/100) * (13/32) + 2300 * (42/100) * (1/3)
= > 234 + 322 = 556
8) Answer: b)
The average number of females working in department B, C and D together
= > [1200 * (52/100) + 1800 * (46/100) + 2000 * (54/100)]/3
= > [624 + 828 + 1080]/3
= > 2532/3 = 844
9) Answer: a)
Total number of females working in department A and E together
= > 1500 * (48/100) + 2300 * (58/100)
= > 720 + 1334 = 2054
Total number of males working in department C and D together
= > 1800 * (54/100) + 2000 * (46/100)
= > 972 + 920 = 1892
Required % = (2054/1892) * 100 = 108.56 % = 109 %
10) Answer: c)
Total number of employees working in department A and B together
= > 1500 + 1200 = 2700
The total number of employees working in department E = 2300
Required % = [(2700 – 2300) / 2300] * 100 = 17.39 % = 17 % more






