Dear IGians,
Miscellaneous problems have become an inevitable part of banking examination now days. In order to enhance your preparation, we are providing you some tricks to solve the miscellaneous problems.
1) There are 5 consecutive odd and 3 consecutive even numbers. The sum of five consecutive odd number is 125 and the lowest even number is 6 more than the twice of average of 5 consecutive odd number. Find the ratio between the lowest odd number and highest even number?
a) 11 : 27
b) 15 : 34
c) 9 : 23
d) 7 : 20
e) None of these
Answer: d)
Let the consecutive odd number be, x, x + 2, x + 4, x + 6, x + 8
X + x + 2 + x + 4 + x + 6 + x + 8 = 125
5x = 125 – 20
5x = 105
X = 21
Average of 5 consecutive odd number = 125/5 = 25
The lowest even number = (2*25) + 6 = 56
The even numbers are, 56, 58 and 60
The ratio between the lowest odd number and highest even number
= > 21 : 60
= > 7 : 20
Shortcut:
The average of 5 consecutive odd number = 125/5 = 25
The average of consecutive number/odd number/even number is always the median. So, the middle odd number is, 25
The odd numbers are, 21, 23, 25, 27, 29
The lowest even number = (2*25) + 6 = 56
The even numbers are, 56, 58 and 60
The ratio between the lowest odd number and highest even number
= > 21 : 60
= > 7 : 20
2) The average age of 26 students in a class is 13 years. If the age of the teacher is included then the average increases by 1 then find the age of the teacher’s son, whose age is (1/5) of teacher’s age?
a) 6 years
b) 11 years
c) 8 years
d) 9 years
e) None of these
Answer: c)
Total age of 26 students = 26*13 = 338
Total age of 26 students and teacher = 27*14 = 378
Age of teacher = 378 – 338 = 40
Age of teacher’s son = (1/5)*40 = 8 years
Shortcut:
N Average
26 13
27 14
If both n and Average increased by 1, then the age of the teacher is,
Age of teacher = (26 + 14) or (27 + 13) = 40 years
Age of teacher’s son = (1/5)*40 = 8 years
3) The average salary of the whole employees (Officers and Clerks) in a company is Rs. 300 per day. The average salary of officers is Rs. 800 per day and that of clerks is Rs. 240 per day. If the number of officers is 30, then find the number of clerks in the company?
a) 180
b) 160
c) 220
d) 250
e) None of these
Answer: d)
Let the number of clerks in the company be x,
800*30 + 240*x = 300*(30 + x)
24000 + 240x = 9000 + 300x
15000 = 60x
X = 15000/60 = 250
Total number of clerks in the company = 250
Shortcut:
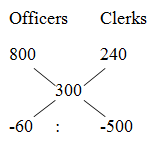
= > 3 : 25
3’s = 30
1’s = 10
Total number of clerks in the company = 25’s = 250
4) Speed of a man in still water is 16 km/hr and the river is running at 6 km/hr. The total time taken to go to a place and come back is 8 hours. Find the distance travelled by the man?
a) 46 km
b) 55 km
c) 42 km
d) 33 km
e) None of these
Answer: b)
Speed of downstream = 16 + 6 = 22 km/hr
Speed of upstream = 16 – 6 = 10 km/hr
Let the distance travelled be x,
(x/22) + (x/10) = 8
X= 55 km
(Or)
Distance = Time *[(Speed of Still water2 – speed of Stream2)/(2*Speed of Still water)]
= > Distance = 8*[(162 – 62)/(2*16)]
= > Distance = 8*[(256 – 36)/32]
= > Distance = 55 km
5) If the length of a rectangle is increased by 20% while the breadth of the rectangle is decreased by 10% then find percentage change in area of the rectangle?
a) 12 % decreased
b) 8 % decreased
c) 12 % increased
d) 8 % increased
e) 21 % decreased
Answer: d)
Let the length and breadth of the rectangle is 10 cm and 10cm,
Previous area= 10*10 = 100
New length= 10*120/100 = 12
New breadth= 10*90/100 = 9
New area= 12*9 = 108
Required percentage = [(108 – 100)/100]*100 = 8 % increased
(Or)
Percentage change = l – b – (lb/100)
= > 20 – 10 – (20*10/100)
= > 8 % increased
6) If 6 men or 9 women can reap a field in 69 days, then what will be the time taken by 10 men and 8 women to reap the field?
a) 30 days
b) 21 days
c) 25 days
d) 27 days
e) None of these
Answer: d)
6 men = 9 women
2 men = 3 women
1 men = (3/2) women
10 m + 8 w = 10*(3/2) w + 8 w = 23 w
Women days
9 69
23 ?
= > (9*69)/23 = 27 days
Shortcut:
Men women days
6 9 69
10 8 ?
Required days
= > (6*9*69)/[(6*8) + (10*9)]
= > (6*9*69)/138
= > 27 days
7) The average marks obtained by 57 students in a certain examination are 24. The average marks of passed students is 26 and the average marks of failed students is 7. Then find the total number of passed students?
a) 49
b) 47
c) 45
d) 51
e) None of these
Answer: d)
Let passed students be x,
According to the question,
57*24 = 26*x + 7*(57 – x)
1368 = 26x + 399 – 7x
969 = 19x
X = 969/19 = 51
Total number of passed students = 51
(Or)
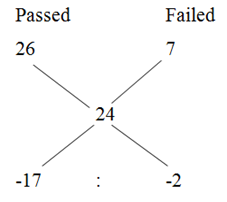
= > 17 : 2
19’s = 57
1’s = 57/19 = 3
Total number of passed students = 17’s = 51
8) Prabha bought two bi-cycles at Rs. 5400. He sells one at 20% profit and another at 25% loss, in the whole transaction there is no profit or loss. Find the difference of the cost price of the bi-cycles?
a) Rs. 450
b) Rs. 540
c) Rs. 640
d) Rs. 360
e) Rs. 600
Answer: e)
Let us take CP of one at x and another at 5400 – x
Given,
X*120/100 + (5400-x)*75/100 = 5400
24x + (5400-x)*15 = 5400*20
= > 9x = 5400*5
= > x = 3000
Required difference= 3000 – 2400 = 600
(Or)
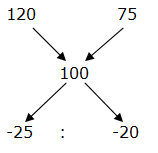
= > 5 : 4
9’s = 5400
1’s = 5400/9 = 600
Required difference = (5 – 4)’s = 1’s = Rs. 600
9) If Ragu purchased some goods for Rs. 2700, and sold one-third of these goods at a loss of 10% then at what gain % should the remaining goods be sold to gain 10% on the whole transaction?
a) 24 %
b) 20 %
c) 15 %
d) 18 %
e) None of these
Answer: b)
2700*(1/3)*(90/100) + 2700*(2/3)*[(x + 100)/100] = (110/100)*2700
810 + 18x + 1800 = 2970
18x = 360
X = 20
Shortcut:
One-third of these goods at a loss of 10% and remaining will be two third goods.
So, the ratio = (1/3): (2/3) = 1: 2
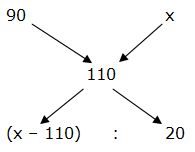
= > (x – 110)/20 = ½
= > x – 110 = 10
= > x = 120 %
So, 2/3rd of the goods will be sold at 20 % profit
10) A customer sold an article at 24% discount on the marked price, yet he got 15% profit on the cost price. If the cost price of the article is Rs. 152, then selling price is what percent of marked price?
a) 84%
b) 70%
c) 76%
d) 80%
e) None of these
Answer: c)
MP*(76/100) = 152*(115/100)
MP = 152*(115/100)*(100/76)
MP = Rs. 230
SP = 230*(76/100)
Required % = ([230*(76/100)]/230)*100 = 76 %
(Or)
SP = MP * (100 – Discount %)/100
(SP/MP)*100 = 100 – 24 = 76%





