Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for LIC AAO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 5603]Click Here to Take LIC AAO Prelims Mock Test
Click Here for Mains 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): In each of the following questions, a question is followed by three statements I, II and III. Read all the statements to find the answer to given question and then answer accordingly that which statement/s can give the answer alone/together.
1) Find the volume of the cone.
- Radius of the base of the cone is equal to the length of the rectangle having area 378 cm2 and breadth 18 cm.
- Height of the cone is 4/3 of its radius.
- Radius of the base of the cone is equal to the side of the square having area 441 cm2.
a) All I, II and III
b) Either I and II or II and III
c) Only I and III
d) Any two of the three
e) Even I, II and III together are not sufficient
2) Find the age of Arohi before six years.
- Ratio of the present ages of Arohi and Nikita is 4:5 respectively. Nikita is four years younger than Kamini.
- After four years, ratio of the ages of Arohi and Kamini will be 5:7 respectively.
- Sum of the present ages of Nikita and Kamini is 44 years.
a) Either I and II or I and III
b) Only II and either I or III
c) All I, II and III
d) Any two of the three
e) Even I, II and III together are not sufficient.
3) Find the time taken by pipe C to fill the tank.
- Pipe A, Pipe B and Pipe C together can fill a tank in 8 minutes. Efficiency of pipe A is double the efficiency of pipe D.
- Pipe A and pipe D together can complete the work in 10 days.
- Pipe B and pipe D together can complete the work in 12 days.
a) Only I and III
b) Only II and III
c) All I, II and III
d) Any two of the three
e) Even I, II and III together are not sufficient.
4) Find the simple interest on the sum at 12% per annum after 8 years.
- Difference between compound interest and simple interest on that sum at 8% per annum after two years is Rs.384.
- Simple interest on that sum at 8% per annum after 4 years will be Rs.19200.
- Compound interest on that sum at 10% per annum after 2 years will be Rs.12600.
a) Only I and III
b) Only II and III
c) Any one of the three
d) Any two of the three
e) Even I, II and III together are not sufficient.
5) Find the probability of drawing two blue balls from the bag.
- The bag contains four different coloured balls. It contains 3 green and 2 red balls.
- The bag contains 5 blue and some yellow balls.
- Probability of drawing one green ball from the bag is 1/6.
a) Only I and II
b) Only II and III
c) All I, II and III
d) Any two of the three
e) Even I, II and III together are not sufficient.
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following table shows the total number of candidates appeared for the examination over the years and the percentage of qualified candidates and the ratio of male and female qualified candidates among them.
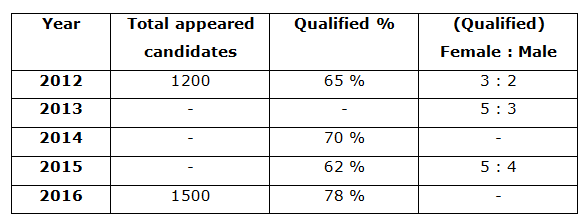
6) If the total number of female qualified candidates in the year 2016 is 520, then the total number of male qualified candidates in the year 2016 is what percentage of total number of female qualified candidates in the same year?
a) 100 %
b) 125 %
c) 85 %
d) 145 %
e) 70 %
7) In 2017, the number of appeared candidates increased by 35 % while comparing with the previous year. If 68 % of appeared candidates in 2017 is qualified in the examination, then find the total number of candidates not qualified in the examination in 2017?
a) 783
b) 721
c) 575
d) 648
e) None of these
8) If the respective ratio of number of appeared candidates to that of qualified candidates in the year 2013 is 5: 4, then the total number of female qualified candidates in the year 2013 is what percent of number of appeared candidates in the same year?
a) 50 %
b) 40 %
c) 65 %
d) 60 %
e) None of these
9) If the number of female qualified candidates in the year 2015 is 620, then find the total number of appeared candidates in the year 2015?
a) 1600
b) 1900
c) 1800
d) 1700
e) None of these
10) If the ratio between the total number of candidates appeared for the examination in the year 2014 to 2016 is 4 : 3 and the total number of male qualified candidates in the year 2013 is 360, then find the difference between the total number of qualified candidates in the year 2014 to that of total number of female qualified candidates in the year 2013?
a) 650
b) 800
c) 750
d) 900
e) None of these
Answers :
Direction (1-5) :
1) Answer: b)
From I and II:
Area of rectangle = length x breadth
=> 378 = length x 18
=> Length = 378/18
=> Length = 21 cm
Radius of the base of the cone = 21 cm
Height = 4/3 x 21 = 28 cm
Volume of cone = 1/3πr2h
= 1/3 x 22/7 x 21 x 21 x 28
= 12936 cm3
From II and III:
Area of square = (side)2
=> 441 = (side)2
=> Side = √441
=> Side = 21 cm
Radius of the base of the cone = 21 cm
Height = 4/3 x 21 = 28 cm
Volume of cone = 1/3πr2h
= 1/3 x 22/7 x 21 x 21 x 28
= 12936 cm3
Hence, Either I and II or II and III sufficient.
2) Answer: a)
From I and II:
Let, the present ages of Arohi and Nikita be 4x years and 5x years respectively.
Kamini = 5x + 4
(4x + 4)/(5x + 4 + 4) = 5/7
=> (4x + 4)/(5x + 8) = 5/7
=> 28x + 28 = 25x + 40
=> 28x – 25x = 40 – 28
=> 3x = 12
=> x = 4
Present age of Arohi = 4x = 4 x 4 = 16 years
Age of Arohi before six years = 16 – 6 = 10 years
From I and III:
Kamini = Nikita + 4
Nikita + Kamini = 40
=> Nikita + Nikita + 4 = 44
=> 2 x Nikita = 44 – 4
=> Nikita = 40/2
=> Nikita = 20 years
Present age of Arohi = 4/5 x 20 = 16 years
Age of Arohi before six years = 16 – 6 = 10 years
Hence, Either I and II or I and III are sufficient.
3) Answer: c)
From I:
1/A + 1/B + 1/C = 1/8
1/A = 2/D
From II:
1/A + 1/D = 1/10
From III:
1/B + 1/D = 1/12
From I, II and III:
1/A + 1/B + 1/C = 1/8 —– (i)
1/A = 2/D —— (ii)
1/A + 1/D = 1/10 —- (iii)
1/B + 1/D = 1/12 —- (iv)
From (ii) and (iii)
2/D + 1/D = 1/10
=> 3/D = 1/10
=> 1/D = 1/30
From (ii)
1/A = 2 x 1/30
=> 1/A = 1/15
From (iv)
1/B + 1/30 = 1/12
=> 1/B = 1/12 – 1/30
=> 1/B = (5 – 2)/60
=> 1/B = 3/60
=> 1/B = 1/20
From (i)
1/15 + 1/20 + 1/C = 1/8
=> 1/C = 1/8 – 1/15 – 1/20
=> 1/C = (15 – 8 – 6)/120
=> 1/C = 1/120
Hence, pipe C can fill the tank in 120 minutes.
Hence, All statement I, II and III are sufficient.
4) Answer: c)
From I:
We know that, for two years
CI – SI = P x (r/100)2
=> 384 = P x (8/100)2
=> P = 384 x 100/8 x 100/8
=> P = Rs.60000
We know that
SI = (P x r x t)/100
= (60000 x 12 x 8)/100
= Rs.57600
From II:
We know that
SI = (P x r x t)/100
19200 = (P x 8 x 4)/100
=> P = 19200 x 100/32
=> P = Rs.60000
We know that
SI = (P x r x t)/100
= (60000 x 12 x 8)/100
= Rs.57600
From III:
We know that
CI = P x (1 + r/100)t – P
=> 12600 = P x (1 + 10/100)2 – P
=> 12600 = P x (1 + 1/10)2 – P
=> 12600 = P x (11/10)2 – P
=> 12600 = P x 121/100 – P
=> 12600 = (121 – 100)P/100
=> 12600 = 21P/100
=> P = 12600 x 100/21
=> P = Rs.60000
(or)
Compound interest for two years = 10 + 10 + (10*10)/100 = 21%
21% = > 12600
100% = > 12600 * (100/21)
Sum = 60000
We know that
SI = (P x r x t)/100
= (60000 x 12 x 8)/100
= Rs.57600
Hence, any one of the three statements is sufficient.
5) Answer: c)
From I:
The bag contains four different coloured balls. It contains 3 green and 2 red balls.
From II:
The bag contains 5 blue and some yellow balls.
From III:
Probability of drawing one green ball from the bag is 1/6.
From I, II and III:
Green = 3
Red = 2
Blue = 5
Let, yellow = n
Total number of balls = 3 + 2 + 5 + n = (10 + n)
3/(10 + n) = 1/6
=> 18 = 10 + n
=> n = 18 – 10
=> n = 8
Total number of balls = 10 + 8 = 18
Required probability = 5c2/18c2
= 10/153
Hence, All I, II and III are sufficient.
Direction (6-10) :
6) Answer: b)
Total number of female qualified candidates in the year 2016 = 520
Total qualified candidates in the year 2016 = 1500*(78/100) = 1170
Total number of male qualified candidates in the year 2016 = 1170 – 520 = 650
Required % = (650/520)*100 = 125 %
7) Answer: d)
Total number of appeared candidates in the year 2017 = 1500*(135/100)
= 2025
Total number of qualified candidates in the year 2017 = 2025*(32/100)
= 648
8) Answer: a)
The ratio of number of appeared candidates to that of qualified candidates
= > 5: 4 (5x, 4x)
The ratio of female to male qualified candidates = 5: 3 (5y, 3y)
4x = 8y (i.e., 5y + 3y)
= > x = 2y
Total appeared candidates = 5x = 10y
Required % = (5y/10y)*100 = 50 %
9) Answer: c)
The number of female qualified candidates in the year 2015 = 620
The ratio of female to that of male qualified candidates in the year 2015 = 5: 4
5’s = 620
1’s = 124
Total number of qualified candidates in the year 2015 = 9’s = 1116
(62/100)*appeared candidates = 1116
Total number of appeared candidates in the year 2015 = 1116*(100/62) = 1800
10) Answer: b)
The ratio of total number of candidates appeared for the examination in the year 2014 to 2016 = 4: 3
Total number of candidates appeared for the examination in the year 2016 =>
3’s = 1500
1’s = 500
Total number of candidates appeared for the examination in the year 2014
= > 4’s = 2000
Total number of candidates qualified for the examination in the year 2014
= > 2000*(70/100) = 1400
The total number of male qualified candidates in the year 2013 = 360
3’s = 360
1’s = 120
Total number of female qualified candidates in the year 2013 = 5’s = 600
Required difference = 1400 – 600 = 800





