Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for LIC AAO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 6492]Click Here to Take LIC AAO Mains Mock Test
Directions (Q. 1 – 5): Study the following information carefully and answer the given questions:
The following table shows the data related to speed of different boats and speed of current. Some values are missing here.
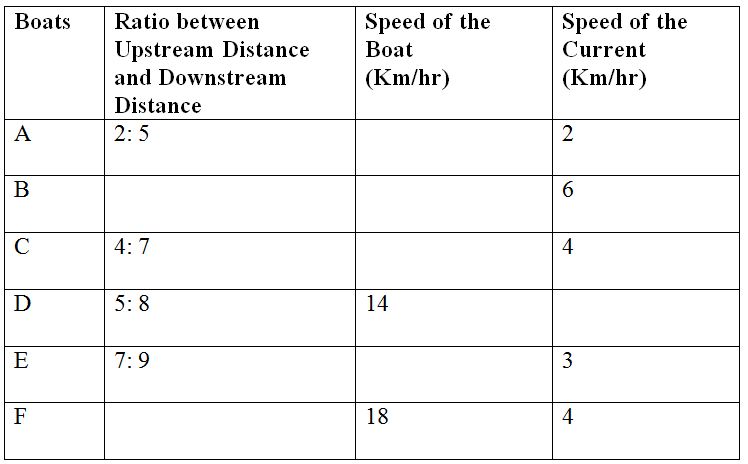
1) If boat A travelled 135 km downstream in 9 hours, then find how much time boat A will take to travel the upstream distance?
a) 24
b) 18
c) 16(1/7)
d) 4(8/9)
e) 4(10/11)
2) If the speed of boat C is 12 km/hr and the time taken to travel upstream distance is 8 hours then find time taken by boat C to travel downstream distance?
a) 2
b) 7
c) 6
d) 8
e) 4
3) If the upstream distance travelled by boat F is ‘x’ while the downstream distance travelled by boat F is ‘x+20’ and the time taken to travel downstream and upstream is equal then find the value of x?
a) 24
b) 18
c) 35
d) 48
e) 40
4) If the total upstream distance travelled by boat B and E in 8 hours is equal to 120 km while the speed of these boats is equal then find time taken by boat E to travel downstream distance of 165 km?
a) 4
b) 10
c) 6
d) 8
e) 11
5) If the ratio between the upstream and downstream speed of boat D is 2:5 and the downstream distance travelled by boat D is 64km then find the time taken by boat D to travel upstream distance?
a) 4
b) 8
c) 6
d) 5
e) 7
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions.
The following table shows the total number of employees in 5 different companies and the percentage of science, commerce and arts graduates among them. Some values are missing here.
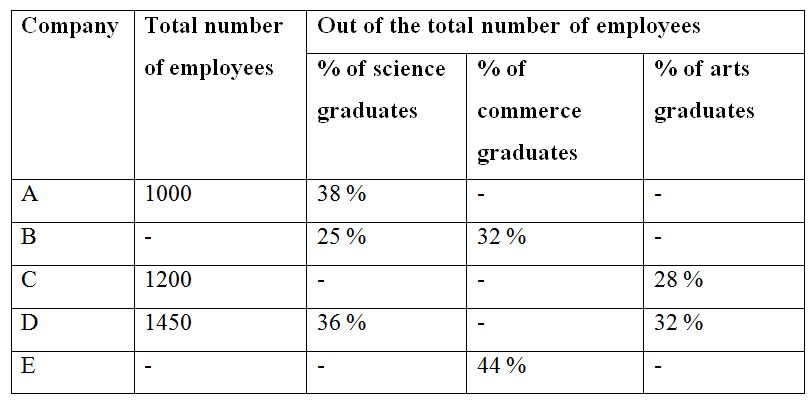
6) Find the ratio between the total number of arts graduates in company A and C together to that of total number of Science graduates in company B and D together, if the total number of commerce graduates in company B is 256 and the percentage of total number of commerce graduates in company A is 32 %?
a) 318 : 361
b) 152 : 167
c) 174 : 185
d) 265 : 342
e) None of these
7) Find the total number of commerce graduates in company A, C and E together, if the percentage of arts graduates in company A and that of science graduates in company C is 30 % and 42 % respectively and the ratio of total number of employees in company A and E is 5 : 8?
a) 1572
b) 1646
c) 1770
d) 1384
e) None of these
8) Find the total number of employees in company E, if the total number of commerce graduates in company C and E together is 1064 and the percentage of science graduates in company C is 42 %?
a) 1800
b) 1600
c) 2200
d) 2400
e) None of these
9) Total number of commerce and arts graduates in company A is approximately what percentage of total number of commerce and arts graduates in company E, if the total number of science graduates in company E is 448, which is equal to 28 % of total number of employees in company E?
a) 72 %
b) 36 %
c) 54 %
d) 90 %
e) None of these
10) Find the difference between the total number of science graduates in company A and B together to that of total number of commerce graduates in company C and D together, if the total number of arts graduates in company B is 344 and the total number of commerce and arts graduates in company C is 696?
a) 244
b) 328
c) 196
d) 372
e) None of these
Answers:
Directions (1-5):
1) Answer: e)
Downstream speed of boat A= 135/9= 15 km/hr
Let the speed of boat A be x
So,
x +2= 15
x= 13kmph
Upstream distance travelled by boat A= 135*2/5= 54km
Upstream speed of boat A= 13-2= 11km/hr
Time taken to travel upstream= 54/11= 4(10/11) hour
2) Answer: b)
Upstream speed of boat C= 12 – 4= 8km/hr
Distance travelled upstream= 8*8= 64km
Downstream distance travelled by boat C= 64*7/4= 112km
Speed downstream= 12+4= 16km/hr
Time taken to travel downstream= 112/16= 7 hours
3) Answer: c)
Speed of boat F downstream= 18+4= 22 km/hr
Speed upstream= 18 – 4= 14 km/hr
Now,
x/ 14 = (x+20) / 22
22x= 14x+280
8x= 280
x = 35km
4) Answer: e)
Let the speed of boat B and E be x
Upstream speed of boat B= x-6
Upstream speed of boat E= x-3
So,
8(x-6) + 8(x-3) = 120
8x – 48 + 8x – 24= 120
16x–72= 120
16x= 192
x = 12km/hr
So,
Downstream speed of boat E= 12+3= 15km/hr
Time taken to travel downstream 165km= 165/15= 11 hours.
5) Answer: d)
Let the speed of the current for boat D be x
Upstream speed= 14-x
Downstream speed= 14+x
So,
(14 – x) / (14+x) = 2/5
70-5x = 28+2x
42 = 7x
x = 6km/hr
Upstream distance travelled by boat D= 64*5/8= 40km
Upstream speed of boat D= 14-6= 8km/hr
Time taken= 40/8= 5 hours.
Directions (6-10):
6) Answer: a)
The total number of arts graduates in company A and C together
= > 1000*(30/100) + 1200*(28/100)
= > 300 + 336 = 636
The total number of Science graduates in company B and D together
= >256*(100/32)*(25/100) + 1450*(36/100)
= > 200 + 522 = 722
Required ratio = 636 : 722 = 318 : 361
7) Answer: d)
The total number of commerce graduates in company A, C and E together
= > [(1000*(32/100) + 1200*(30/100) + (1000/5)*8*(44/100)]
= > [320 + 360 + 704] = 1384
8) Answer: b)
The total number of commerce graduates in company C and E together = 1064
Total number of commerce graduates in company C
= > 1200*(30/100) = 360
Total number of commerce graduates in company E
= > 1064 – 360 = 704
According to the question,
(44/100)*Total employees in company E = 704
Total employees in company E = 704*(100/44) = 1600
9) Answer: c)
Total number of commerce and arts graduates in company A
= > 1000*(62/100) = 620
Total number of commerce and arts graduates in company E
= > (448/28)*100*(72/100) = 1152
Required % = (620/1152)*100 = 53.819 % = 54 %
10) Answer: a)
The total number of science graduates in company A and B together
= >1000*(38/100) + (344/43)*100*(25/100)
= > 380 + 200 = 580
Total number of commerce graduates in company C
= > 696 – 1200*(28/100)
= > 696 – 336 = 360
The total number of commerce graduates in company C and D together
= >360 + 1450*(32/100)
= > 360 + 464 = 824
Required difference = 824 – 580 = 244





