Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7396]Data Interpretation
Directions (1 – 5): Study the following information carefully and answer the questions give below:
The following table contains information about seven mixtures. Some data in the table are missing.
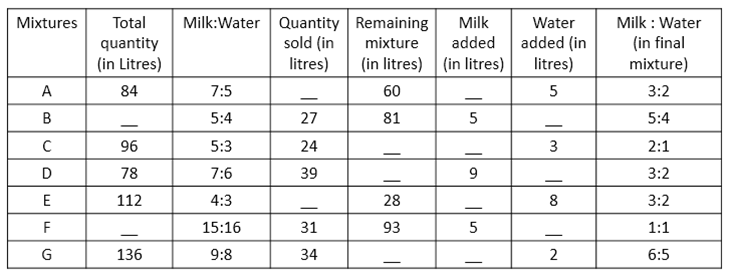
1) Quantity of milk in the final mixture A is what percent of amount of water in the final mixture B?
a) 85.5%
b) 72.5%
c) 112.5%
d) 98.5%
e) None of these
2) Find the respective ratio of amount of milk in final mixture C and amount of water in final mixture D.
a) 5:2
b) 4:3
c) 3:1
d) 3:2
e) None of these
3) Another mixture H contains amount of milk equal to 20% more than the amount of milk in the final mixture E and water equal to 40% more than the amount of water in the final mixture E. Find the difference between total quantity of mixture H and final quantity of mixture E.
a) 12 litres
b) 14 litres
c) 15 litres
d) 18 litres
e) None of these
4) Find the sum of the quantities of milk in all the final mixtures.
a) 515 litres
b) 415 litres
c) 325 litres
d) 225 litres
e) None of these
5) A mixture K contains amount of milk equal to 25% more than the amount of milk in final mixture G and amount of water equal to 10% less than the amount of water in the final mixture C. The milkman sold 34 litres of the mixture and added 10 litres of milk and 12 litres of water to the remaining mixture. Find the difference between quantity of milk and quantity of water in the final mixture K.
a) 25 litres
b) 30 litres
c) 40 litres
d) 50 litres
e) None of these
Caselet
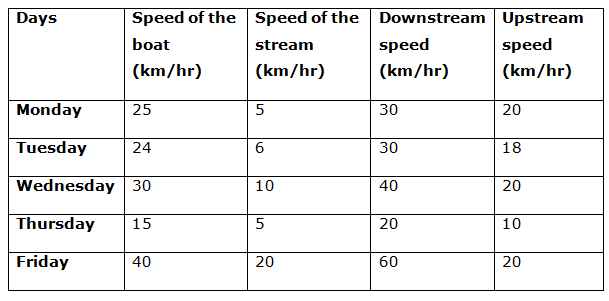
Directions (6 – 10): Following is the information about the upstream speed and downstream speeds of a boat on different days of a week.
Monday: Downstream speed is 50% more than the upstream speed. Time taken to cover 120 km along the stream is same as the time taken to cover 80 km against the stream. If the downstream speed is increased by 10 km/hr, then the boat takes 3 hours to cover 120 km.
Tuesday: Speed of the stream is one-fourth of the speed of the boat. Time taken to cover 150 km along the stream is 5 hours.
Wednesday: Downstream speed is 100% more than the upstream speed. Time taken to cover 200 km along the stream in 5 hours.
Thursday: Stream of the speed is one – third of the speed of the boat. The difference between the downstream speed and upstream speed is 10 km/hr. Time taken to cover 140 km along the stream is same as the 70 km against the stream.
Friday: Speed of the stream is 20 km/hr which is half of the speed of the boat.
6) If on Saturday speed of boat in still water was 50% of the sum of speeds of boat in still water on Monday and Thursday and speed of stream was double the speed of stream on Monday, then how much time will the boat take to cover total upstream distance, which is average of upstream distance covered by all the boat in 5 hours in all 5 days together?
a) 8.4 hours
b) 7.2 hours
c) 6.4 hours
d) 8.8 hours
- e) None of these
7) If both, speed of boat in still water and speed of stream on Wednesday are increased by 20% each, and then find the percentage increase in upstream and downstream journey time together?
Statement I: Initially, distance covered by the boat on Wednesday is 200 km along the stream and 100 km against the stream.
Statement II: Total time taken to cover downstream and upstream distance by boat on Wednesday is 10 hours.
a) Only II
b) Only I
c) Both I and II
d) Neither I nor II
e) Either I or II
8) Quantity I: Total upstream distance covered by all the given boat in all the 5 days together in 10 hours.
Quantity II: Total downstream distance covered by all the given boat in all the 5 days together in 5 hours.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II
9) If speed of boat in still water on Sunday was 50% of sum of the speeds of boat in still water on Tuesday and Friday, speed of stream on Sunday was half of the speed of stream on Friday. What was the average speed of upstream and downstream journeys on Sunday?
a) 32 km/hr
b) 30 km/hr
c) 34 km/hr
d) 36 km/hr
e) None of these
10) Quantity I: Average speed of the boat on Friday is what percentage more/less than the average speed of the boat on Monday?
Quantity II: Average speed of the boat on Tuesday is what percentage more/less than the average speed of the boat on Thursday?
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II
Answers :
Directions (1-5) :
1) Answer: c)
Quantity of milk in the remaining mixture A = 7/12 x 60 = 35 litres
Quantity of water in the remaining mixture A = 5/12 x 60 = 25 litres
Let, the amount of milk added to the remaining mixture A = n litres
(35 + n)/(25 + 5) = 3/2
=> 2 x (35 + n) = 3 x 30
=> 70 + 2n = 90
=> 2n = 90 – 70
=> 2n = 20
=> n = 20/2
=> n = 10 litres
Quantity of milk in the final mixture A = 35 + 10 = 45 litres
Quantity of milk in the remaining mixture B = 5/9 x 81 = 45 litres
Quantity of water in the remaining mixture B = 4/9 x 81 = 36 litres
Let the amount of water added to the remaining mixture B = k litres
(45 + 5)/(36 + k) = 5/4
=> 4 x 50 = 5 x (36 + k)
=> 200 = 180 + 5k
=> 5k = 200 – 180
=> 5k = 20
=> k = 4 litres
Quantity of water in the final mixture B = 36 + 4 = 40 litres
Required percentage = 45/40 x 100 = 112.5%
2) Answer: c)
Remaining mixture C = 96 – 24 = 72 litres
Quantity of milk in the remaining mixture C = 5/8 x 72 = 45 litres
Quantity of water in the remaining mixture C = 3/8 x 72 = 27 litres
Let the amount of milk added to the remaining mixture = l litres
(45 + l)/(27 + 3) = 2/1
=> 45 + l = 2 x 30
=> l = 60 – 45
=> l = 15 litres
Quantity of milk in the final mixture C = 45 + 15 = 60 litres
Remaining mixture D = 78 – 39 = 39 litres
Quantity of milk in the remaining mixture D = 7/13 x 39 = 21 litres
Quantity of water in the remaining mixture D = 6/13 x 39 = 18 litres
Let, the amount of water added to the remaining mixture D = m litres
(21 + 9)/(18 + m) = 3/2
=> 2 x 30 = 3 x (18 + m)
=> 60 = 54 + 3m
=> 3m = 60 – 54
=> 3m = 6
=> m = 2
Amount of water in the final mixture D = 18 + 2 = 20 litres
Required ratio = 60: 20 = 3:1
3) Answer: b)
Amount of milk in the remaining mixture E = 4/7 x 28 = 16 litres
Amount of water in the remaining mixture E = 3/7 x 28 = 12 litres
Let the amount of milk added to the remaining mixture E = p litres
(16 + p)/(12 + 8) = 3/2
=> 2 x (16 + p) = 20 x 3
=> 32 + 2p = 60
=> 2p = 60 – 32
=> 2p = 28
=> p = 28/2
=> p = 14 litres
Amount of milk in the final mixture E = 16 + 14 = 30 litres
Amount of water in the final mixture E = 12 + 8 = 20 litres
Total amount of final mixture E = 30 + 20 = 50 litres
Amount of milk in mixture H = 30 x 120/100 = 36 litres
Amount of water in mixture H = 20 x 140/100 = 28 litres
Total amount of mixture H = 36 + 28 = 64 litres
Required difference = 64 – 50 = 14 litres
4) Answer: c)
Quantity of milk in the remaining mixture A = 7/12 x 60 = 35 litres
Quantity of water in the remaining mixture A = 5/12 x 60 = 25 litres
Let, the amount of milk added to the remaining mixture A = n litres
(35 + n)/(25 + 5) = 3/2
=> 2 x (35 + n) = 3 x 30
=> 70 + 2n = 90
=> 2n = 90 – 70
=> 2n = 20
=> n = 20/2
=> n = 10 litres
Quantity of milk in the final mixture A = 35 + 10 = 45 litres
Quantity of milk in the remaining mixture B = 5/9 x 81 = 45 litres
Quantity of milk in the final mixture B = 45 + 5 = 50 litres
Remaining mixture C = 96 – 24 = 72 litres
Quantity of milk in the remaining mixture C = 5/8 x 72 = 45 litres
Quantity of water in the remaining mixture C = 3/8 x 72 = 27 litres
Let the amount of milk added to the remaining mixture = l litres
(45 + l)/(27 + 3) = 2/1
=> 45 + l = 2 x 30
=> l = 60 – 45
=> l = 15 litres
Quantity of milk in the final mixture C = 45 + 15 = 60 litres
Remaining mixture D = 78 – 39 = 39 litres
Quantity of milk in the remaining mixture D = 7/13 x 39 = 21 litres
Quantity of milk in the final mixture D = 21 + 9 = 30 litres
Quantity of milk in the remaining mixture E = 4/7 x 28 = 16 litres
Quantity of water in the remaining mixture E = 3/7 x 28 = 12 litres
Let the amount of milk added to the remaining mixture E = p litres
(16 + p)/(12 + 8) = 3/2
=> 2 x (16 + p) = 20 x 3
=> 32 + 2p = 60
=> 2p = 60 – 32
=> 2p = 28
=> p = 28/2
=> p = 14 litres
Quantity of milk in the final mixture E = 16 + 14 = 30 litres
Quantity of milk in the remaining mixture F = 15/31 x 93 = 45 litres
Quantity of milk in the final mixture F = 45 + 5 = 50 litres
Remaining mixture G = 136 – 34 = 102 litres
Quantity of milk in the remaining mixture G = 9/17 x 102 = 54 litres
Quantity of water in the remaining mixture G = 8/17 x 102 = 48 litres
Let the amount of milk added to remaining mixture G = y litres
(54 + y)/(48 + 2) = 6/5
=> (54 + y)/50 = 6/5
=> 5 x (54 + y) = 300
=> 270 + 5y = 300
=> 5y = 30
=> y = 6
Quantity of milk in the final mixture G = 54 + 6 = 60 litres
Required sum = 45 + 50 + 60 + 30 + 30 + 50 + 60 = 325 litres
5) Answer: b)
Remaining mixture G = 136 – 34 = 102 litres
Quantity of milk in the remaining mixture G = 9/17 x 102 = 54 litres
Quantity of water in the remaining mixture G = 8/17 x 102 = 48 litres
Let the amount of milk added to remaining mixture G = y litres
(54 + y)/(48 + 2) = 6/5
=> (54 + y)/50 = 6/5
=> 5 x (54 + y) = 300
=> 270 + 5y = 300
=> 5y = 30
=> y = 6
Quantity of milk in the final mixture G = 54 + 6 = 60 litres
Quantity of milk in mixture K = 60 x 125/100 = 75 litres
Quantity of water in the remaining mixture C = 3/8 x 72 = 27 litres
Quantity of water in the final mixture C = 27 + 3 = 30 litres
Quantity of water in mixture K = 30 x 90/100 = 27 litres
Total quantity of mixture K = 75 + 27 = 102 litres
Milk: water = 75:27 = 25:9
Remaining quantity of mixture K = 102 – 34 = 68 litres
Quantity of milk in the remaining mixture K = 25/34 x 68 = 50 litres
Quantity of water in the remaining mixture K = 9/34 x 68 = 18 litres
Quantity of milk in the final mixture K = 50 + 10 = 60 litres
Quantity of water in the final mixture K = 18 + 12 = 30 litres
Required difference = 60 – 30 = 30 litres
Directions (6 – 10):
Monday:
Ratio of downstream speed to upstream speed = 150: 100
= 3: 2
If the downstream speed is increased by 10 km/hr, then the boat takes 3 hours to cover 120 km.
Downstream speed = 3x + 10
According to the statement,
120/(3x+10) = 3
120 = 3*(3x + 10)
40 = 3x + 10
= > 3x = 30
= > x = 10 km/hr
Downstream speed = 3*10 = 30 km/hr
Upstream speed = 2*10 = 20 km/hr
Speed of the boat = ½ * (Downstream speed + Upstream speed)
= ½ *(30 + 20)
= ½ * 50 = 25 km/hr
Speed of the stream = ½ * (Downstream speed – Upstream speed)
= ½ * (30 – 20)
= ½ * 10 = 5 km/hr
Tuesday:
Ratio of the speed of the boat to speed of the stream = x: 1/4*x
= 4: 1
Downstream speed = 150/5 = 30 km/hr
Downstream speed = (4x + x) = 5x = 30 km/hr
= > x = 30/5 = 6 km/hr
Upstream speed = (4x – x) = 3x = 3 * 6 = 18 km/hr
Speed of the boat = ½ * (Downstream speed + Upstream speed)
= ½ * (30 + 18)
= ½ * 48 = 24 km/hr
Speed of the stream = ½*(Downstream speed – Upstream speed)
= ½ * (30 – 18)
= ½ * 12 = 6 km/hr
Wednesday:
Ratio of downstream speed to upstream speed = 200: 100 = 2: 1
Downstream speed = 200/5 = 40 km/hr
Upstream speed = 40/2 * 1 = 20 km/hr
Speed of the boat = ½ * (Downstream speed + Upstream speed)
= ½* (40 + 20)
= ½ * 60 = 30 km/hr
Speed of the stream = ½*(Downstream speed – Upstream speed)
= ½ * (40 – 20)
= ½ * 20 = 10 km/hr
Thursday:
Ratio of the speed of the boat to speed of the stream = x: 1/3*x
= 3: 1
Downstream speed = (3x +x) = 4x
Upstream speed = (3x – x) = 2x
Downstream speed – Upstream speed = 4x – 2x = 10 km/hr
2x = 10
= > x = 5 km/hr
Downstream speed = 5 * 4 = 20 km/hr
Upstream speed = 2 * 5 = 10 km/hr
Speed of the boat = 3x = 15 km/hr
Speed of the stream = x = 5 km/hr
Friday:
Ratio of the speed of the boat to the speed of the stream = 2: 1
Speed of the stream = 20 km/hr
Speed of the boat = 20/1 * 2 = 40 km/hr
Downstream speed = (Speed of the boat + Speed of the stream)
= (40 + 20) = 60 km/hr
Upstream speed = (Speed of the boat – Speed of the stream)
= (40 – 20) = 20 km/hr
6) Answer: d)
Speed of boat on Saturday = 50/100 *(25 + 15)
= 40/2 = 20 km/hr
Speed of the stream on Wednesday = 2*5 = 10 km/hr
Upstream speed = 20 – 10 = 10 km/hr
Total upstream distance covered by all the given boat in 5 days
= (20 + 18 + 20 + 10 + 20)*5
= 88*5 = 440 km
Average of upstream distance covered by all the boat in 5 hours in all 5 days together
= 440/5 = 88 km
Required time = 88/10 = 8.8 hours
7) Answer: b)
New speed of boat on Wednesday = 120/100 * 30
= 36 km/hr
New speed of stream on Wednesday = 120/100 * 10
= 12 km/hr
Downstream speed = 36 + 12 = 48 km/hr
Upstream speed = 36 – 12 = 24 km/hr
From I,
Total time taken by boat on Wednesday = 200/40 + 100/20
= 5 + 5 = 10 hours
New total time taken by boat on Wednesday = 200/48 + 100/24
= (400/48) = 25/3 hours
Required percentage = [(10 – 25/3) / 10] * 100 = 50/3 %
Hence, statement I alone is sufficient to answer the given question.
From II,
From statement II, we don’t have any other information about total distance covered by boat initially.
Hence, statement II alone is not sufficient to answer the given question.
8) Answer: b)
Quantity I: Total upstream distance covered by all the given boat in all the 5 days together in 10 hours.
Total upstream distance in all the given 5 days
= 10 *(20+18+20+10+20)
= 10*88 = 880 km
Quantity II: Total downstream distance covered by all the given boat in all the 5 days together in 5 hours.
Total downstream distance in all the given 5 days
= 5 * (30+30+40+20+60)
= 5 * 180
= 900 km
Hence, Quantity I < Quantity II
9) Answer: e)
Speed of the boat on Sunday = 50/100 * (24 + 40) = 32 km/hr
Speed of the stream on Sunday = ½ * 20 = 10 km/hr
Downstream speed = 32 + 10 = 42 km/hr
Upstream speed = 32 – 10 = 22 km/hr
Average speed = 2 * 42 * 22/(42 + 22)
= 231/8 km/hr
10) Answer: b)
Quantity I: Average speed of the boat on Friday is what percentage more/less than the average speed of the boat on Monday?
Average speed of the boat on Friday
= 2 * 60 * 20/(60 + 20)
= 2400/80
= 30 km/hr
Average speed of the boat on Monday
= 2 * 30 * 20/(30 + 20)
= 24 km/hr
Required percentage
= [(30 – 24)/24] * 100
= 25%
Quantity II: Average speed of the boat on Tuesday is what percentage more/less than the average speed of the boat on Thursday?
Average speed of the boat on Tuesday
= 2 * 30 * 18/(30 + 18)
= 22.5 km/hr
Average speed of the boat on Thursday
= 2 * 20*10/(20+10)
= 400/30 = 40/3 km/hr
Required percentage = [(22.5 – 40/3)/(40/3)] * 100
= [(27.5*3)/(40*3)] * 100
= 68.75%
Hence, Quantity I < Quantity II





