Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for LIC AAO/SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 5506]Click Here to Take LIC AAO Prelims Mock Test
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 2): Each question contains a statement followed by Quantity I, II and III. Read the information clearly and answer your questions accordingly.
The options represent the relations between these three quantities
A) >
B) <
C) =
D) ≤
E) ≥
For example:
Quantity I = 200
Quantity II = 300
Quantity III = 100
Hence, Quantity I < Quantity II > Quantity III
a) A, B
b) B, C
c) B, A
d) E, B
e) B, D
Answer is option: c)
1) Present age of P is 6 years more than the age of Q after 7 years. The present age of R is 3 times of present age of Q. The ratio of age of R, 3 years ago to that of the present age of S is 3: 4. Present age of T is one-eleventh of the present age of S.
Quantity I:Find the age of S, 8 years ago, if the present age of Q is 12 years?
Quantity II:Find the present age of R, if the present age of P is square of five?
Quantity III:Find the sum of the present age of P and Q together, if the present age of R is 36 years?
a) D, A
b) B, D
c) C, B
d) A, C
e) D, D
2) A, B and C entered into a partnership by investing in the ratio of 4: 7: 9 respectively. After 4 months, A invested 30 % more than the initial investment. And after another 5 months, B withdraws Rs. 5000 but C invested Rs. 10000 more. The ratio of share of A, B and C is 192: 275: 370.
Quantity I: A and P entered into a partnership by investing in the ratio of 2: 3. Find the share of P, if the total profit at the end of the year is Rs. 200000?
Quantity II: Find the share of B, if the total profit at the end of the year for A, B and C is Rs. 669600?
Quantity III: Find the75 % of the share of C, if the total profit at the end of the year for A, B and C is Rs. 1004400?
a) B, B
b) A, D
c) E, C
d) A, C
e) E, B
Directions (Q. 3 – 5): In the following questions, two equations I and II are given. You have to solve both the equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
3)
I) x3 – 133 = [56 % of 1250] ÷ 4 + 113 + 124 × 9 ÷ 2
II) y2 – y – 72 = 0
4)
I) 2x2 – x – 66 = 0
II) 3y2 – 5y – 42 = 0
5)
I) 6x + 4y = 4x + 7y
II) 5x + 3y + 5 = 2x + 5y
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following table shows the total number of car spare parts (In lakhs) manufactured by five different companies in a certain year and total number of defective and sold items are given.
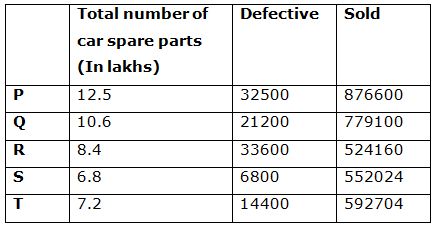
6) Total number of defective car spare parts of company P, R and T together is approximately what percentage of total number of defective car spare parts of company Q, S and T together?
a) 150 %
b) 170 %
c) 190 %
d) 210 %
e) 230 %
7) Find the ratio of total number of unsold spare parts in company Q to that of company R?
a) 312: 409
b) 265: 288
c) 124: 133
d) 156: 141
e) None of these
8) Find the difference between the total number of car spare parts sold by Company P and R together to that Company Q and T together?
a) 75420
b) 84564
c) 79128
d) 28956
e) None of these
9) How much percentage of car spare parts sold by Company Q?
a) 73.5 %
b) 81 %
c) 84 %
d) 77.5 %
e) None of these
10) Find the average number of car spare parts manufactured by all the given companies together?
a) 8.6 lakhs
b) 7.7 lakhs
c) 9.1 lakhs
d) 7.3 lakhs
e) None of these
Answers:
Directions (1-2):
1) Answer: c)
Present age of P = The age of Q, after 7 years + 6
The ratio of present age of R and Q = 3: 1
The ratio of age of R, 3 years ago to that of the present age of S = 3: 4
Present age of T = (1/11)*the present age of S
Quantity I:Find the age of S, 8 years ago, if the present age of Q is 12 years?
The present age of Q = 12 years
Present age of R = 12*3 = 36 years
The age of R, 3 years ago = 33 years
Present age of S = (33/3)*4 = 44 years
The age of S, 8 years ago = 44 – 8 = 36 years
Quantity II:Find the present age of R, if the present age of P is square of five?
Present age of P = 52 = 25 years
The age of Q, after 7 years = 25 – 6 = 19 years
Present age of Q = 12 years
The ratio of present age of R and Q = 3: 1
Present age of R = 12*3 = 36 years
Quantity III: Find the sum of the present age of P and Q together, if the present age of R is 36 years?
Present age of R = 36 years
Present age of Q = (36/3) = 12 years
Present age of P = 19 + 6 = 25 years
Required sum = 12 + 25 = 37 years
36 = 36 < 37
Quantity I = Quantity II < Quantity III
2) Answer: a)
The share of A, B and C
= > [4x*4 + 4x*(130/100)*8]: [7x*9 + (7x – 5000)*3]: [9x*9 + (9x + 10000)*3] = 192:275: 370
= > [16x + 208x/5]: [63x + 21x – 15000]: [81x + 27x + 30000] = 192:275: 370
= > [288x/5]: [84x – 15000]: [108x + 30000] = 192:275: 370
According to the question,
= > (84x – 15000)/(108x + 30000) = (275/370)
= > 6216x – 1110000 = 5940x + 1650000
= > 276x = 2760000
= > x = 10000
Initial investment of A = 4x = Rs. 40000
Initial investment of B = 7x = Rs. 70000
Initial investment of C = 9x = Rs. 90000
Quantity I: A and P entered into a partnership by investing in the ratio of 2: 3. Find the share of P, if the total profit at the end of the year is Rs. 200000?
The share of A and P
= > [40000*12] : [(40000/2)*3*12]
= > 2 : 3
5’s = 200000
1’s = 40000
The share of P = Rs. 120000
(Or)
Period of investment is same for both of them. So,
The ratio of profit = 2 : 3
5’s = 200000
1’s = 40000
The share of P = Rs. 120000
Quantity II: Find the share of B, if the total profit at the end of the year for A, B and C is Rs. 669600?
The share of A, B and C
= >192:275: 370
Total profit = 837’s = 669600
1’s = 800
The share of B = 275’s = Rs. 220000
Quantity III: Find the75 % of the share of C, if the total profit at the end of the year for A, B and C is Rs. 1004400?
The share of A, B and C
= > 192 : 275 : 370
Total profit = 837’s = 1004400
1’s = 1200
The share of C = 370’s = Rs. 444000
Required share = 444000*(75/100) = Rs. 333000
120000 < 220000 < 333000
Directions (3-5):
3) Answer: a)
I) x3 – 133 = [56 % of 1250] ÷ 4 + 113 + 124 × 9 ÷ 2
X3 = (56/100)*(1250/4) + 1331 + (124*9)/2 + 133
X3 = 175 + 1331 + 558 + 133 = 2197
X = 13
II) y2 – y – 72 = 0
(y – 9) (y + 8) = 0
Y = 9, -8
X > y
4) Answer: e)
I) 2x2 – x – 66 = 0
2x2 – 12x + 11x – 66 = 0
2x (x – 6) + 11(x – 6) = 0
(2x + 11) (x – 6) = 0
X = -11/2, 6 = -5.5, 6
II) 3y2 – 5y – 42 = 0
3y2 + 9y – 14y – 42 = 0
3y (y + 3) – 14 (y + 3) = 0
(3y – 14) (y + 3) = 0
Y = 14/3, -3 = 4.66, -3
Can’t be determined
5) Answer: c)
I) 6x + 4y = 4x + 7y
2x – 3y = 0 —> (1)
II) 5x + 3y + 5 = 2x + 5y
3x – 2y = -5 —> (2)
By solving the equation (1) and (2), we get,
X = -3, y = -2
X < y
Directions (6-10):
6) Answer: c)
Total number of defective car spare parts of company P, R and T together
= > 32500 + 33600 + 14400 = 80500
Total number of defective car spare parts of company Q, S and T together
= > 21200 + 6800 + 14400 = 42400
Required % = (80500/42400)*100 = 190 %
7) Answer: b)
Total number of unsold car spare parts in company Q
= > 1060000 – (21200 + 779100) = 259700
Total number of unsold car spare parts in company R
= > 840000 – (33600 + 524160) = 282240
Required ratio = 259700 : 282240 = 265 : 288
8) Answer: d)
The total number of car spare parts sold by Company P and R together
= > 876600 + 524160 = 1400760
The total number of car spare parts sold by Company Q and T together
= > 779100 + 592704 = 1371804
Required difference = 1400760 – 1371804 = 28956
9) Answer: a)
Required % = (779100/1060000)*100 = 73.5 %
10) Answer: c)
The total number of car spare parts manufactured by all the given companies together
= > 12.5 + 10.6 + 8.4 + 6.8 + 7.2 = 45.5 lakhs
Required average = (45.5/5) = 9.1 lakhs





