Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for LIC AAO/SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 5615]Click Here to Take LIC AAO Prelims Mock Test
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
1) A, B and C started a business by investing Rs. 25000, Rs. 40000 and Rs. 30000 respectively. After 6 months C withdraws Rs. 12000 while A invested Rs. 3000 more. If the total profit at the end of the year is Rs. 144800, then the share of A will exceed that of C by?
a) Rs. 4000
b) Rs. 2500
c) Rs. 3000
d) Rs. 2000
e) None of these
2) The simple interest accrued on an amount of Rs. 28000 at the end of 3 years is Rs. 6720. What would be the corresponding compound interest?
a) Rs. 7893.524
b) Rs. 7519.128
c) Rs. 7271.936
d) Rs. 7052.252
e) None of these
3) Perimeter of a rectangle is x meter and circumference of a circle is 8 meter more than the perimeter of the rectangle. Ratio of radius of circle and length of the rectangle is 7: 12 and ratio of length and breadth of rectangle is 3: 2. Find the area of the rectangle?
a) 418 Sq m
b) 352 Sq m
c) 436 Sq m
d) 384 Sq m
e) None of these
4) Rajesh borrowed Rs. 60000 from a bank at the rate of 8 % per annum for two years at simple interest and lends the same money to Mahesh at the rate of 8 % for two years but he charged compound interest. Find the overall gain of Rajesh?
a) Rs. 412
b) Rs. 384
c) Rs. 396
d) Rs. 438
e) None of these
5) 5 years ago, the age of Aruna is equal to the age of Preethi, 10 years ago. 5 years hence the ratio of ages of Aruna and Preethi is 6: 7. Find the present age of Aruna?
a) 40 years
b) 30 years
c) 35 years
d) 25 years
e) None of these
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
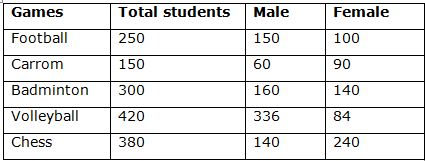
There are 1500 students in a college. All the students were participating in different games in the cultural event. The games are Football, carrom, Volleyball, Badminton, Chess. Total number of males is 192 more than the total number of females. The percentage of males participated in football is 60 % of total number of students participated in football. Total males participated in carrom is two-third of the total females participated in carrom. Total females participated in football is 100. The ratio of total students participated in carrom to that of Badminton is 1: 2. Total students participated in Carrom is 100 less than the total students participated in football. Total number of females participated in Volleyball is 20 % of total students participated in volleyball. Total students participated in Carrom is 10 more than the total females participated in Badminton. Total males participated in Volleyball is 336. Total females participated in Chess is 100 more than the total males participated in Chess.
6) Find the average number of students participated in Football, Badminton and Chess together?
a) 280
b) 310
c) 350
d) 240
e) None of these
7) Find the difference between the total males participated in Carrom and Badminton together to that of total females participated in Volleyball and Chess together?
a) 128
b) 135
c) 142
d) 104
e) None of these
8) Find the ratio between the total males participated in Chess to that of total students participated in Volleyball?
a) 2: 6
b) 3: 8
c) 11: 19
d) 23: 27
e) None of these
9) Total males participated in Football is what percentage of total females participated in Carrom?
a) 152.33 %
b) 135.25 %
c) 166.67 %
d) 106.18 %
e) 124.52 %
10) Find the difference between the average number of males participated in Carrom and Volleyball together to that of the average number of females participated in Football and Badminton together?
a) 84
b) 72
c) 66
d) 78
e) None of these
Answers:
1) Answer: a)
The share of A, B and C
= > (25000*6 + 28000*6): (40000*12): (30000*6 + 18000*6)
= > 318000: 480000: 288000
= > 53: 80: 48
181’s = 144800
1’s = 800
The difference between the shares of A to that of C
= > 5’s = 5*800 = Rs. 4000
2) Answer: c)
S.I = PNR/100
6720 = (28000*3*R)/100
R = (6720*100)/(28000*3) = 8 %
C.I = P*(1 + (R/100))n – 1)
= > 28000*(1 + (8/100))3 – 1)
= > 28000*((108/100)3 – 1)
= > 28000*((27/25)3 – 1)
= > 28000*[(19683/15625) – 1]
= > 28000*(4058/15625)
= > Rs. 7271.936
3) Answer: d)
Perimeter of rectangle = 2*( l + b) = x
2l + 2b = x and 2πr = x + 8
r/l = 7/12 and l/b = 3/2
r : l : b = 7 : 12 : 8 (7y, 12y, 8y)
2πr = x + 8
2πr = 2l + 2b + 8
2*(22/7)*7y = 2*12y + 2*8y + 8
44y = 24y + 16y + 8
44y – 40y = 8
4y = 8
Y = 2
Length of the rectangle = 12y = 24 m
Breadth of the rectangle = 8y = 16 m
The area of the rectangle = l*b = 24*16 = 384 Sq m
4) Answer: b)
The difference between the simple interest and compound interest for 2 years,
Diff = Sum*(r/100)2
So, the overall gain of Rajesh = 60000*(8/100)2 = Rs. 384
5) Answer: d)
5 years hence, Aruna: Preethi = 6: 7 (6x, 7x)
5 years ago, the age of Aruna is equal to the age of Preethi, 10 years ago
= > (6x – 10) = (7x – 15)
= > x = 5
The present age of Aruna = 6x – 5 = 25 years
Directions (Q. 6 – 10):
Total students = 1500
Total number of males = 192 + Total number of females
Total males – Total females = 192 —- (1)
Total males + Total females = 1500 —- (2)
Solve the equation (1) and (2), we get
Total males = 846
Total females = 654
Football:
The percentage of males participated in football
= > 60 % of total number of students participated in football
Total females participated in football = 100
(40/100)*Total students participated in football = 100
Total students participated in football = 100*(100/40) = 250
Total males participated in football = 250 – 100 = 150
Carrom:
Total males participated in carrom = (2/3)*total females participated in carrom
The ratio of male to that of females participated in Carrom = 2: 3
Total students participated in Carrom
= > The total students participated in football – 100
= > 250 – 100 = 150
Total males participated in carrom = (150/5)*2 = 60
Total females participated in carrom = 150 – 60 = 90
Badminton:
The ratio of total students participated in carrom to that of Badminton = 1: 2
Total students participated in Badminton = (150/1)*2 = 300
Total students participated in Carrom = 10 + The total females participated in Badminton
150 – 10 = The total females participated in Badminton
The total females participated in Badminton = 140
The total males participated in Badminton = 300 – 140 = 160
Volleyball:
Total number of females participated in Volleyball = (20/100)*total students participated in volleyball
Total males participated in Volleyball = 336
336 = (80/100)* total students participated in volleyball
Total students participated in Volleyball = 336*(100/80) = 420
Total females participated in Volleyball = 420 – 336 = 84
Chess:
Total females participated in Chess = 100 + The total males participated in Chess
Total students participated in Chess = 1500 – (250 + 150 + 300 + 420) = 380
F + M = 380 –> (1)
F – M = 100 –> (2)
By solving the equation (1) and (2),
F = 240, M = 140
6) Answer: b)
The average number of students participated in Football, Badminton and Chess together
= > (250 + 300 + 380)/3
= > 930/3 = 310
7) Answer: d)
The total males participated in Carrom and Badminton together
= > 60 + 160 = 220
The total females participated in Volleyball and Chess together
= > 84 + 240 = 324
Required difference = 324 – 220 = 104
8) Answer: a)
The total males participated in Chess = 140
The total students participated in Volleyball = 420
Required ratio = 140: 420 = 2: 6
9) Answer: c)
Total males participated in Football = 150
Total females participated in Carrom = 90
Required % = (150/90)*100 = 500/3 = 166.67 %
10) Answer: d)
The average number of males participated in Carrom and Volleyball together
= > (60 + 336)/2 = 396/2 = 198
The average number of females participated in Football and Badminton together
= > (100 + 140)/2 = 240/2 = 120
Required difference = 198 – 120 = 78





