Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for SBI Clerk Mains 2020 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Ensure Your Ability Before the Exam – Take SBI Clerk 2020 Mains Free Mock Test
Data Interpretation
Directions (1 – 5): Study the following information carefully and answer the given questions?
The pie chart shows the total employees working in different departments in a company and the line graph shows the percentage of graduate employees among them.
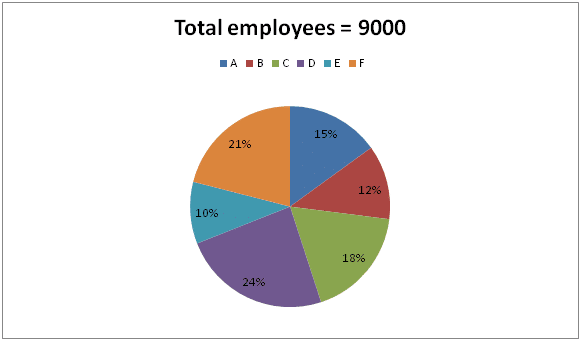
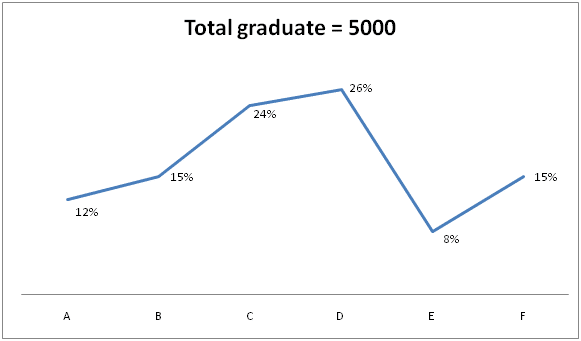
1) Find the difference between the total number of graduate employees in company A to that of total number of non graduate employees in company D?
a) 340
b) 260
c) 420
d) 580
e) None of these
2) Find the average number of graduate employees in company A, B and C together?
a) 2800
b) 1950
c) 3100
d) 2550
e) None of these
3) Find the ratio between the total employees in company C to that of total non graduate employees in company E and F together?
a) 81: 82
b) 53: 57
c) 11: 13
d) 75: 79
e) None of these
4) Total employees in company D and F together is what percentage of total non graduate employees in company A and B together?
a) 250 %
b) 425 %
c) 375 %
d) 180 %
e) None of these
5) Find the difference between the average employees in company D, E and F together to that of total non graduate employees in company B, C and F together?
a) 850
b) 740
c) 930
d) 1020
e) None of these
Quantity based questions
Directions (6 – 10): Each question contains a statement followed by Quantity I, quantity II and Quantity III. Which of the following should be placed in the blank spaces of the expression “Quantity I __ Quantity II ___ Quantity III” from left to right with respect to the given statements?
6) Quantity I: (840 – 384) ÷ 24 + 787 =?
Quantity II: 45 % of 600 – 18 % of 350 =? – 62 – 252
Quantity III: ? = (3745 + 1780) ÷ 17 + 162 + (5/11) of 880 – 15
a) >, <
b) >, >
c) <, <
d) =, >
e) None of these
7) Quantity I: 38 % of 350 + 400 % of 16 =? % of 50
Quantity II: 156 ÷ 13 + ∛19683 – (12 × 15) =? – 83
Quantity III: (√2500)3 =?
a) >, =
b) >, <
c) =, <
d) =, =
e) None of these
8) Quantity I: x2 – 17x + 72 = 0
Quantity II: y2 -19y + 88 = 0
Quantity III: 3x2 + 26x + 56 = 0
a) >, =
b) ≥, =
c) ≤, ≤
d) <, <
e) None of these
9) Quantity I: 578, 600, 630, 669, 718, ?
Quantity II: 8, 9, 14, 51, 188, ? , 5754
Quantity III: 56, 114, ? , 1384, 6925, 41556
a) <, <
b) >, >
c) =, >
d) <, >
e) None of these
10) A contains 4 pink, 6 red and 5 blue colour balls.
Quantity I: Two balls are taken randomly from the bag; find the probability of getting both is blue?
Quantity II: Two balls are taken randomly from the bag, find the probability of getting at least one pink ball
Quantity III: Two balls are taken randomly from the bag; find the probability of getting one red and one pink
a) <, >
b) >, >
c) <, <
d) =, =
e) None of these
Answers :
Directions (1-5) :
1) Answer: B
The total number of graduate employees in company A
= > 5000 * (12/100) = 600
The total number of non graduate employees in company D
= > [9000 * (24/100)] – [5000 * (26/100)]
= > 2160 – 1300 = 860
Required difference = 860 – 600 = 260
2) Answer: D
The average number of graduate employees in company A, B and C together
= > 5000 * (51/100) = 2550
3) Answer: A
The total employees in company C
= > 9000 * (18/100) = 1620
The total non graduate employees in company E and F together
= > {[9000 * (10/100) – 5000 * (8/100)] + [(9000 * (21/100) – 5000 * (15/100)]}
= > {[900 – 400] + [1890 – 750]}
= > 500 + 1140 = 1640
Required ratio = 1620: 1640 = 81: 82
4) Answer: C
Total employees in company D and F together
= > 9000 * (45/100) = 4050
Total non graduate employees in company A and B together
= > {[9000 * (15/100) – 5000 * (12/100)] + [9000 * (12/100) – 5000 * (15/100)]}
= > {[1350 – 600] + [1080 – 750]}
= > 750 + 330 = 1080
Required % = (4050 / 1080) * 100 = 375 %
5) Answer: D
The average employees in company D, E and F together
= > 9000 * (55/100) * (1/3) = 1650
The total non graduate employees in company B, C and F together
= > {[9000 * (12/100) – 5000 * (15/100)] + [9000 * (18/100) – 5000 * (24/100)] + [9000 * (21/100) – 5000 * (15/100)]} * (1/3)
= > {[1080 – 750] + [1620 – 1200] + [1890 – 1140]} * (1/3)
= > (330 + 420 + 1140) / 3 = 1890 / 3
= > 630
Required difference = 1650 – 630 = 1020
Directions (6-10) :
6) Answer: C
Quantity I:
(840 – 384) / 24 + 787 = x
x = 456 / 24 + 787
x = 20 + 787 = 807 = 810
Quantity II:
45 % of 600 – 18 % of 350 = x – 62 – 252
(45/100) * 600 – (18/100) * 350 + 62 + 625 = x
x = 270 – 63 + 62 + 625
x = 894
Quantity III:
x = (3745 + 1780) ÷ 17 + 162 + (5/11) of 880 – 15
x = 5525/17 + 256 + (5/11) * 880 – 15
x = 325 + 256 + 400 – 15
x = 966
Hence, Quantity I < Quantity II < Quantity III
7) Answer: B
Quantity I:
38 % of 350 + 400 % of 16 = x % of 50
(38/100) * 350 + (400/100)*16 = (x/100) * 50
133 + 64 = x/2
197*2 = x
x = 394
Quantity II:
156 ÷ 13 + ∛19683 – (12 × 15) = x – 83
(156/13) + 27 – (12*15) + 512 = x
x = 12 + 27 – 180 + 512
x = 371
Quantity III:
(√2500)3 =?
(50)3 =?
125000 =?
Hence, Quantity I > Quantity II < Quantity III
8) Answer: E
Quantity I:
x2 – 17x + 72 = 0
(x – 8) (x – 9) = 0
x = 8, 9
Quantity II:
y2 -20y + 99 = 0
(y – 11) (y – 9) = 0
y = 11, 9
Quantity III:
3x2 + 26x + 56 = 0
3x2 + 12x + 14x + 56 = 0
3x(x + 4) + 14(x + 4) = 0
(3x + 14) (x + 4) = 0
x = -14/3, -4 = -4.667, -4
Hence, Quantity I ≤ Quantity II > Quantity III
9) Answer: D
Quantity I:
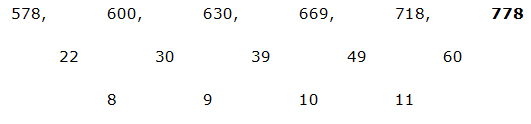
The difference of difference is, 8, 9, 10, 11,..
The answer is, 778
Quantity II:
The pattern is, * 1 + 12, * 2 – 22, * 3 + 32, * 4 – 42, * 5 + 52, * 6 – 62,…
The answer is, 965
Quantity III:
The pattern is, * 2 + 2, * 3 + 3, * 4 + 4, * 5 + 5, * 6 + 6,…
The answer is, 345
Hence, Quantity I < Quantity II > Quantity III
10) Answer: A
Quantity I:
Required probability = 5C2/15C2
= (5 * 4)/(15 * 14)
= 2/21 = 0.095
Quantity II:
Required probability = 1 – (None pink)
= 1 – 11C2/15C2
= 1 – [(11 * 10)/(15 * 14)]
= 1 – 11/21 = 10/21 = 0.476
Quantity III: Two balls are taken randomly from the bag; find the probability of getting one red and one pink
Required probability = (6C1 * 4C1)/15C2
= (6 * 4)/(15 * 14)
= 4/35 = 0.114
Hence, Quantity I < Quantity II > Quantity III
| Check Here to View SBI Clerk Mains 2020 Quantitative Aptitude Questions | ||
| Day 06 | Day 05 | Day 04 |
| Click Here for SBI Clerk 2020 – Detailed Exam Notification | ||





