SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5160]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following information carefully and answer the questions give below:
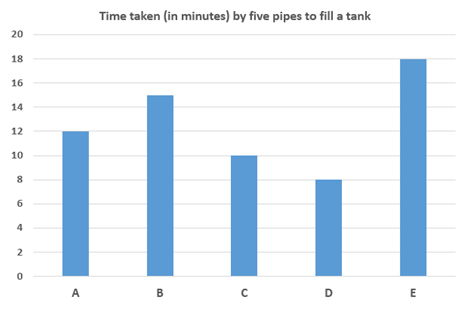
The bar graph 1 shows the time taken by five pipes (A, B, C, D and E) to fill a tank
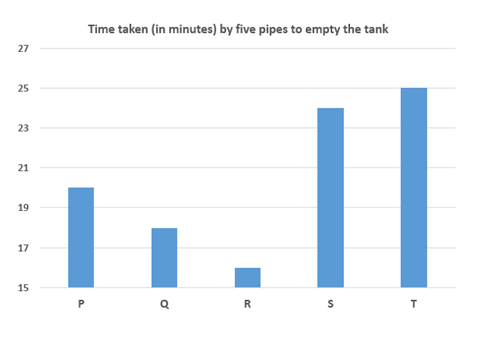
The bar graph 2 shows the time taken by five pipes (P, Q, R, S and T) to empty the tank
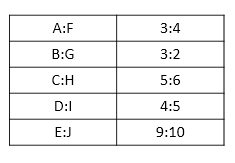
The following table shows the ratio of time taken by pipes to fill the tank.
1) Pipe A and Pipe B opened simultaneously for 4 minutes, then closed and then pipe F and pipe Q are opened for 2 minutes, and then closed. Find the time taken by pipe G to fill the remaining part of the tank.
a) 7 minutes
b) 139/36 minutes
c) 5 minutes
d) 178/39 minutes
e) None of these
2) Efficiency of pipe K is twice the efficiency of pipe A and efficiency of pipe L is 1.5 times the efficiency of pipe S. Pipe C and pipe K are opened simultaneously for 3 minutes and then closed. Find the time taken by pipe L and pipe R together to empty the filled part of the tank.
a) 4 minutes
b) 47/12 minutes
c) 32/5 minutes
d) 5 minutes
e) None of these
3) Time taken by pipe M to fill the tank is 20% more than the time taken by pipe I to fill the tank and efficiency of pipe N is twice the efficiency of pipe J. Time taken by pipe M and pipe N to fill the tank is what percent of the time taken by pipe D and pipe E together to fill the tank.
a) 67.67%
b) 74.44%
c) 98.48%
d) 81.14%
e) 83.33%
4) Find the respective ratio of time taken by pipe B, pipe G and pipe P together to fill the tank to that of time taken by pipe E, pipe H and pipe S together to fill the tank.
a) 4:5
b) 5:6
c) 6:7
d) 3:4
e) None of these
5) Pipe A, pipe C and pipe E are opened simultaneously for 4 minutes then closed and pipe P and pipe S are opened for 2 minutes then closed. Find the time taken by pipe G and pipe J to fill the remaining part of the tank.
a) 27/13 days
b) 41/27 days
c) 31/11 days
d) 51/29 days
e) None of these
Directions (6 – 10): Study the following and answer the following questions.
The following table shows that the data of 6 employees of ABC company.
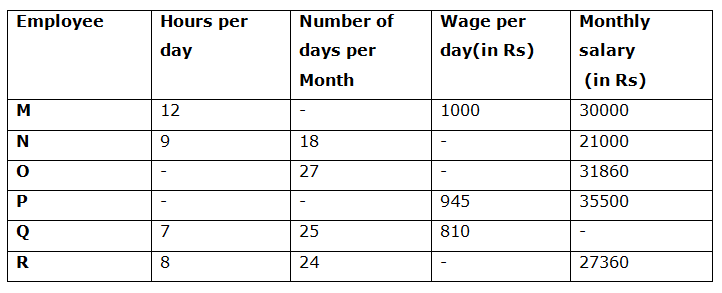
6) The employee P is twice as good as the employee R and hence he can finish a work in 10 days less than the employee R, then how much a company has to pay to both of them if they work together to do the same piece of work?
a) Rs 13900
b) Rs 43000
c) Rs 23000
d) Rs 21000
e) Rs 13000
7) The employee Q does 75% of the work in 18 days, and then he assisted the employee O to finish the work in 4 days. Then the amount paid to the employee O per annum if he would have completed the work alone is approximately what percentage more or less than the employee Q’s one year salary.
a) 150%
b) 130%
c) 110%
d) 180%
e) 187%
8) If N and R together can do a piece of work in 15 days, and they worked for 9 days, then N left. After another 8 days, R finished the remaining work. Then find the total wage received by the employee R if he alone has finished the whole work?
a) Rs 34700
b) Rs 25000
c) Rs 33600
d) Rs 22800
e) Rs 13200
9) If the employees M, Q and R can do a piece of work in 240 hours, 420 hours and 240 hours respectively, then in how many days can the employee M do the work if he is assisted by Q and R on every third day?
a) 14 days
b) 15 days
c) 34 days
d) 18 days
e) 17 days
10) The employee P can do a certain work in the same time period in which N and Q together can do the same work. If N and P together could do it in 30 days and Q alone in 60 days, find the ratio of a number of days taken by the employees P to that of the employee N.
a) 1:2
b) 2:3
c) 1:6
d) 1:5
e) 1:3
Answers :
Direction (1-5) :
1) Answer: b)
Part of the tank filled by pipe A in one minute = 1/12
Part of the tank filled by pipe B in one minute = 1/15
Time taken by pipe F to fill the tank = 4/3 x 12 = 16 minutes
Part of the tank filled by pipe F in one minute = 1/16
Time taken by pipe G to fill the tank = 2/3 x 15 = 10 minutes
Part of the tank filled by pipe G in one minute = 1/10
Part of the tank emptied by pipe Q in one minute = 1/18
Let required time = t minutes
According to the question
4/15 + 4/12 + 2/16 – 2/18 + t/10 = 1
=> t/10 = 1 – 4/15 – 1/3 – 1/8 + 1/9
=> t/10 = (360 – 120 – 90 – 45 + 40)/360
=> t/10 = 139/360
=> t = 139/360 x 10
=> t = 139/36 minutes
2) Answer: c)
Part of the tank filled by pipe A in one minute = 1/12
Part of the tank filled by pipe K in one minute = 2/12 = 1/6
Part of the tank filled by pipe C in one minute = 1/10
Part of the tank emptied by pipe S in one minute = 1/24
Part of the tank emptied by pipe L in one minute = 1.5/24 = 1/16
Part of the tank emptied by pipe R in one minute = 1/16
Part of the tank filled by pipe C and pipe K in 3 minutes = 3/10 + 3/6
= (9 + 15)/30
= 24/30
Let the required time taken = t minutes
t/16 + t/16 = 24/30
=> 2t/16 = 24/30
=> t = 24/30 x 16/2
=> t = 32/5 minutes
3) Answer: c)
Time taken by pipe I to fill the tank = 5/4 x 8 = 10 minutes
Part of the tank filled by pipe I in one minute = 1/10
Time taken by pipe M to fill the tank = 10 x 120/100 = 12 minutes
Part of the tank filled by pipe M in one minute = 1/12
Time taken by pipe J to fill the tank = 10/9 x 18 = 20 minutes
Part of the tank filled by pipe J in one minute = 1/20
Part of the tank filled by pipe N in one minute = 2/20 = 1/10
Part of the tank filled by pipe D in one minute = 1/8
Part of the tank filled by pipe E in one minute = 1/18
Let the time taken by pipe M and pipe N to fill the tank = t minutes
And the time taken by pipe D and pipe E to fill the tank = k minutes
t/12 + t/10 = 1
=> (5t + 6t)/60 = 1
=> 11t/60 = 1
=> t = 60/11 minutes
And
k/8 + k/18 = 1
(9k + 4k)/72 = 1
=> k = 72/13 minutes
Required percentage = (60/11)/(72/13) x 100
= 60/11 x 13/72 x 100
= 98.48%
4) Answer: b)
Part of the tank filled by pipe B in one minute = 1/15
Time taken by pipe G to fill the tank = 2/3 x 15 = 10 minutes
Part of the tank filled by pipe G in one minute = 1/10
Part of the tank emptied by pipe P in one minute = 1/20
Part of the tank filled by pipe E in one minute = 1/18
Time taken by pipe H to fill the tank = 6/5 x 10 = 12 minutes
Part of the tank filled by pipe H in one minute = 1/12
Part of the tank emptied by pipe S in one minute = 1/24
Let the time taken by pipe B, pipe g and pipe P together to fill the tank = t minutes
And the time taken by pipe E, pipe H and pipe S together to fill the tank = k minutes
t/15 + t/10 – t/20 = 1
=> (4t + 6t – 3t)/60 = 1
=> 7t/60 = 1
=> t = 60/7 minutes
And
k/18 + k/12 – k/24 = 1
=> (4k + 6k – 3k)/72 = 1
=> 7k/72 = 1
=> k = 72/7 minutes
Required ratio = 60/7: 72/7 = 5:6
5) Answer: b)
Part of the tank filled by pipe A in one minute = 1/12
Part of the tank filled by pipe C in one minute = 1/10
Part of the tank filled by pipe E in one minute = 1/18
Part of the tank emptied by pipe P in one minute = 1/20
Part of the tank emptied by pipe S in one minute = 1/24
Time taken by pipe G to fill the tank = 2/3 x 15 = 10 minutes
Part of the tank filled by pipe G in one minute = 1/10
Time taken by pipe J to fill the tank = 10/9 x 18 = 20 minutes
Part of the tank filled by pipe J in one minute = 1/20
Let the required time taken = t minutes
4/12 + 4/10 + 4/18 – 2/20 – 2/24 + t/10 + t/20 = 1
=>1/3 + 2/5 + 2/9 – 1/10 – 1/12 + (2t + t)/20 = 1
=> (60 + 72 + 40 – 18 – 15)/180 + 3t/20 = 1
=> 139/180 + 3t/20 = 1
=> 3t/20 = 1 – 139/180
=> 3t/20 = (180 – 139)/180
=> 3t/20 = 41/180
=> t = 41/180 x 20/3
=> t = 41/27 days
Direction (6-10) :
6) Answer: a)
Given that, the ratio of time taken by the employees P and R= 1:2
If R takes 20 days to complete the work, then the number of days taken by P to complete the work= 10 days
Now, the part of the work completed by employees P and R in 1 day= (1/10+1/20) = 3/20
(i.e) The employees P and R can complete the work in 20/3 days.
Now, the Total amount received by P=945*20/3=Rs 6300
And one day wage of the employee R= 27360/24=Rs 1140
Then Total amount received by the employee R= 1140*20/3=Rs 7600
Hence total amount paid by the company= 6300+7600= Rs 13900
7) Answer: e)
Number of days taken by the employee Q to finish the whole work= 18*100/75 =18* 4/3 = 24 days
Now remaining work= 1- ¾= ¼
Thus, ¼ of the work is done by O and Q in 4 days.
Then Whole work can be completed by O and Q in 16 days
Now, work done by O in one day= 1/16-1/24
= 1/48
Now the wage of the employee O for one day= 31860/27=Rs 1180
Then total annual salary received by the employee O for 48 days = 1180*48*12
= Rs 679680
One year salary of the employee Q = 810*24*12 = 233280
Required percentage= (436680/233280)*100
=187%
8) Answer: d)
Since N and R worked together for 9 days,
The part of the work completed by N and R in 9 days= (1/15)*9=3/5
Now remaining work= 1-3/5= 2/5
(i.e) 2/5 part of the work is done by R in 8 days.
Then whole work will be done by R= 8*5/2
= 20 days
From the table, we have, the Monthly salary of R= Rs 27360
Then salary of the employee per day= 27360/24=Rs 1140
Hence total wage received by the employee R for 20 days= 1140*20=Rs 22800
9) Answer: b)
Given that the employee M can finish the work in 240 hours. (i.e) 240/12= 20 days
Similarly, the employee Q can finish the work in 420 hours (i.e) 420/7 = 60 days
And the employee R can finish the work in 240 hours. (i.e) 240/8 = 30 days
The work was done by the employee in 2 days= 1/20*2= 1/10
Then the work was done by the employees M, Q and R=1/20+1/60+1/30
= 1/10
Thus work done in 3 days= 1/10+1/10
= 1/5
Hence The whole work can be completed in 3*5 days.(i.e) 15 days.
10) Answer: e)
Given that, Work done by the employees P and N in one day= 1/30 and Q’s one day work= 1/60
Then work done by all the three employees in one day= (1/30+1/60)
= 1/20
Given that, P’s one-day work= work done by N and Q together in one day.
Then we have,
2* (P’s one day work) = 1/20
Then P’s one day work= 1/40
From this we have,
N’s one day work = 1/30-1/40
= 1/120
(i.e) N alone can complete the work in 120 days.
Then required ratio= 40:120
= 1:3





