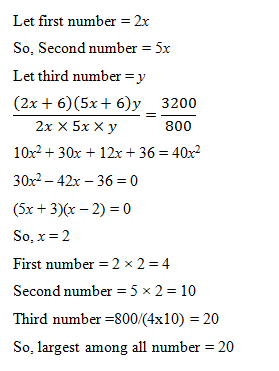Dear Aspirants, Here we have given the Important SSC CGL Exam 2018 Practice Test Papers. Candidates those who are preparing for SSC CGL 2018 can practice these questions to get more confidence to Crack SSC CGL 2018 Examination.
[WpProQuiz 3132]Click “Start Quiz” to attend these Questions and view Explanation
1) If x and y are irrational numbers, then x + y xy is
a) A real number
b) A complex number
c) A rational number
d) An irrational number
2) Simplify: 77 x 325 + 37 x 555 – 40 x 325
a) 32690
b) 32560
c) 22555
d) 54330
3) If 3x+4y+ 2z =2 0 and 8a – y + z = 4, then find the value of x+y+z = ?
a) 5
b) 2
c) 16
d) Cannot be determined
4) There are n persons who can do a job in 27 days. But due to some reasons, 6 persons did not come for the work. The remaining persons took 18 days to complete half of the work. What is the value of n?
a) 19
b) 18
c) 25
d) 24
5) In a company, the salary of a sales executive is partly fixed and partly based on his sales. A sales executive earns Rs. 22000 in a month for selling 300 units and Rs. 20000 in the next month for selling 250 units. If he sells 400 units in a month then how much amount he earns per unit?
a) 125
b) 65
c) 200
d) 150
6) _____________is equivalent to right ___________whose base is a circle.
a) Square, rectangle
b) Square, cylinder
c) Cone, pyramid
d) None of the above
7) The nature of roots of the equation is 10x2 – 6x + 1 = 0
a) Real and equal
b) Imaginary
c) Rational and unequal
d) Rational and equal
8) Catherine was born when her father was 20 years old. At present the product of ages of Catherine and her father is 125, what will be Catherine’s age after five years?
a) 5 years
b) 10 years
c) 15 years
d) 25 years
9) The product of three integers is 800. The ratio of first and second is 2 : 5. If 6 is added both the first and the second and third remains unaltered. The product becomes 3200. The greatest of the three integers is
a) 80
b) 40
c) 20
d) 10
10) If x = 3cosA.cosB, y = 3 cosA.sinB and z = 3sinA, then the value of x2 + y2 + z2 is
a) 32
b) 10
c) 18
d) 9
Answers :
1). Answer: a)
If x = √2, y = – √2then x + y – xy = √2 –√2 – (√2) (–√2) = 2
If x = √2, y = √3 then x + y – xy = √2 + √3 – (√2) (√3) = √2 + √3 – √6
We can conclude that x + y – xy is a real number.
2). Answer: b)
77 x 325 + 37 x 555 – 40 x 325
3). Answer: d)
Here, No. of unknowns is not equal to No. of equations.
Hence the answer cannot be determined
4). Answer: d)
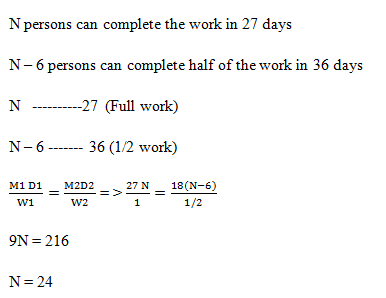
5). Answer: b)
Let the salary be Rs. x and commission is Rs. y per unit sold.
X+300y= 22000
X+250 y= 20000
Solving two equations, y = 40
Total for 400 units = x + 400y
=> X + 300 y + 100 y = 22000 +100 x 40 = 26000
Average earning per unit= 26000 / 400 = 65
6). Answer: c)
7). Answer: b)
B2 – 4AC = 36 – 4(10) (1) = – 4
As B2– 4AC is negative the roots are imaginary.
8). Answer: b)
Let Catherine’s age be x years
Her father’s age = (x+20) years
X (x+20) = 125
X = – 25 or 5
Catherine’s age after five years = 5+5 = 10 years
9). Answer: c)
10). Answer: d)
x2 + y2 + z2 = (3cosAcosB)2 + (3cosA.sinB)2 + (3sinA)2
= 9cos2A (cos2B + sin2B) + 9sin2A
= 9(sin2A + cos2A)
= 9