Dear Aspirants, Here we have given the Important SSC Exam 2018 Practice Test Papers. Candidates those who are preparing for SSC 2018 can practice these questions to get more confidence to Crack SSC 2018 Examination.
[WpProQuiz 4153]Click here to view Quantitative Aptitude Questions in Hindi
1) The difference between the simple interest on a certain amount at the rate of 20% per annum for 1.5 years and compound interest at the same rate but compounded every 6 months is Rs.155. What is the principal sum?
a) Rs.4000
b) Rs.5000
c) Rs.6000
d) None of these
2) The marks scored by a student in three subjects are in the ratio of 4:5:6. If the candidate scored an overall aggregate of 60% of the sum of the maximum marks in all three subjects is the same, in how many subjects did he score more than 60%?
a) 1
b) 2
c) 3
d) None of these
3) A man, a woman, a boy and a girl can do a piece of work in 4, 6, 12 and 24 days, respectively. How many girls are required to work with 1 man, 1 woman and 1 boy in complete the work in 1 day?
a) 8
b) 15
c) 10
d) 12
4) Two shots are fired from a gun carriage with a gap of 30 minutes between the two shots. A biker moving away from the gun carriage heard the second shot 33 minutes after first one. What is the ratio of the speed of sound to that of the biker?
a) 30 : 1
b) 11 : 1
c) 15 : 2
d) 20 : 3
5) A can swim at 10 kmph in still water. If the velocity of water is 4 kmph and it takes him 10 hours to swim to a place and come back, how far is the place?
a) 24 km
b) 32 km
c) 42 km
d) None of these
6) Suppose a, b and c are in Arithmetic Progression and a², b² and c² are in Geometric Progression. If a < b < c and a + b + c = , then the value of a is equal to:
a) 1/2√2
b) 1/2√3
c) (1/2) – (1/√3
d) (1/2 – 1/√2)
7) Sum of the series 1² – 2² + 3² – 4² + … + 2001² – 2002² + 2003² is:
a) 2007006
b) 1005004
c) 200506
d) None of these
8) The interior angles of a polygon are in Arithmetic Progression. If the smallest angle is 120º and common difference is 5º, then number of sides in the polygon is:
a) 7
b) 8
c) 9
d) None of these
9) If the positive real numbers a, b and c are in Arithmetic Progression, such that abc = 4, then minimum possible value of b is
a) 2 3/2
b) 22/3
c) 21/3
d) None of these
10) If one root of the equation ax² + bx + c = 0 is double of the other, then 2b² is equal to
a) 9ca
b) c√2a
c) 2√3 ac
d) None of these
11) A pole has to be erected on the boundary of a circular park of diameter 13m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 m. The distance of the pole from one of the gate is:
a) 8 m
b) 8.25 m
c) 5 m
d) None of the above
12)
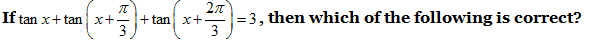
a) tan x = 1
b) tan 2x = 1
c) tan 3x = 1
d) None of the above
13) If D is the midpoint of side BC of a DABC and AD is the perpendicular to AC, then
a) 3AC² = BC² – AB²
b) 3BC² = AC² – 3AB²
c) BC² + AC² = 5AB²
d) None of these
14) A cylinder, a hemisphere and a cone stand on the same base and have the heights. The ratio of the areas of their curved surface is
a) 2 : 2 : 1
b) 2 : √2 : 1
c) √2: 3 : 1
d) None of these
15) If each, α, β, γ is positive acute angle such that sin (α + β – γ) = 1/ = 1/√2, cosec (β + γ – α) = 2/ √3 and tan (γ + α – β) = 1/√3. What are the values of α, β, γ?
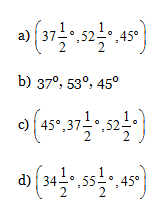
Answers :
1) Answer: b)
We can solve this problem by checking the options:
Simple interest for Rs.5000 would be 30% of 5000 = Rs.1500
Compound interest for Rs.5000 = 500 + 550 + 605 = Rs.1655
Required difference = Rs. (1655 – 1500) = Rs.155.
2) Answer :a)
Let the maximum marks in each of the three subjects be 100.
Therefore, the candidate scored an aggregate of 60% of 3 × 100 = 60% of 300 marks. = 180 marks
Let the marks scored in the three subjects be 4 x, 5x and 6x.
Then, 4x + 5x + 6x = 180; or 15x = 180; or, x = 12
Therefore, marks scored by the candidate in the three subjects are 4 × 12, 5 × 12 and 6 × 12 = 48, 60 and 72.
Hence, the candidate has scored more than 60% in one subject.
3) Answer :d)
Let the total work be 240 units (LCM of 4, 6, 12, 24).
Efficiencies per day of:
Man = 240/4 = 60 units
Woman = 240/6 = 40 units
Boy = 240/12 = 20 units
And girl = 240/24 = 10 units
In one day, a man, a woman and a boy can do 120 units. The remaining 120 units can be done by 12 girls in that same day.
4) Answer :b)
Let y be the speed of sound and x the speed of the man.
Then the relative speed of sound = y – x
Or, y – x = 30/33 of y
Or, 33y – 33x = 30y
Or, y/x = 11/1
Hence, y: x = 11: 1.
5) Answer: d)
Let the place is d km away from the original position of A. According to the question,

Now by putting the options in the above equation or by solving the above equation, we get d = 42 km.
6) Answer: d)
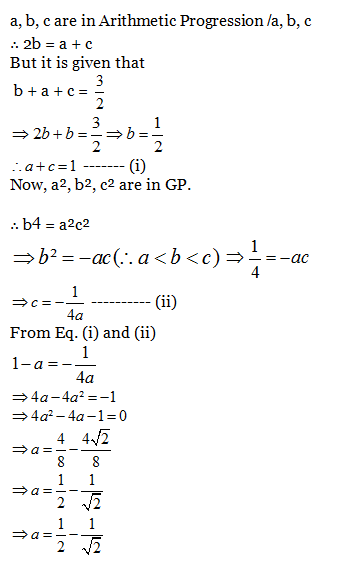
7) Answer: a)
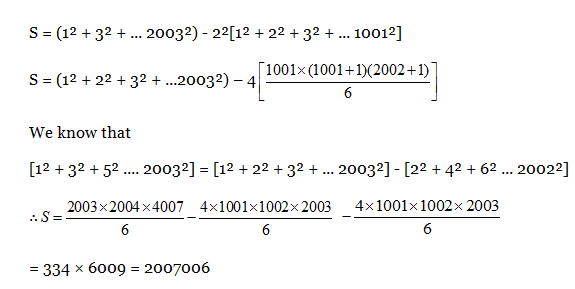
8) Answer: c)
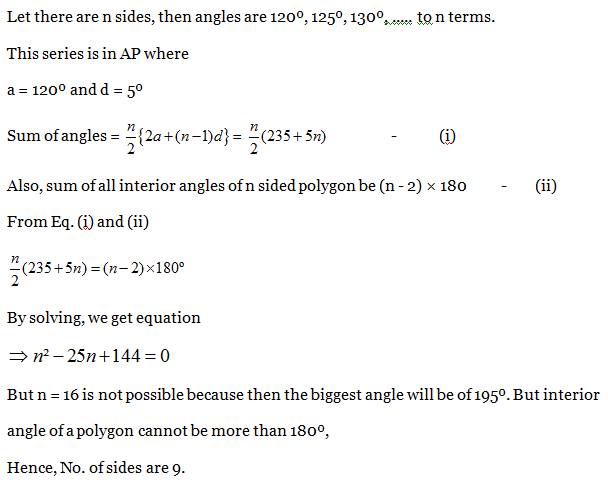
9) Answer: b)
a b c = 4 and a, b, c are in AP.
Then, value of b will be minimum when all three are equal.
∴ b³ = 4
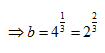
10) Answer: a)
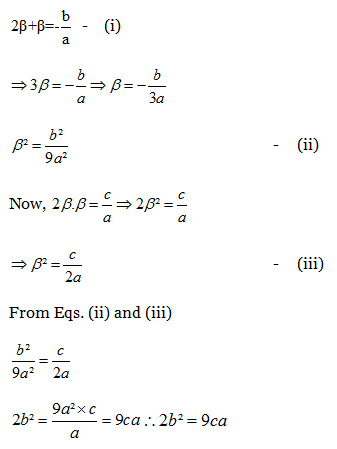
11) Answer: c)
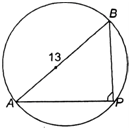
Let P be the required location of the pole.
Let the distance of the pole from the gate B be x m i.e., BP = x meter.
Now the difference of the distance of the pole from the two gates
= AP – BP = 7 m.
∴ AP = (x+ 7) m
Since ∴ P is an angle in semi-circle;
∴ ∠ P = 90º and AB = 13 m (diameter of circle)
AB² = AP² + BP² [∴ in right-angled ∆ABP]
–> (13)² = (x + 7)² + x²
–> 169 = x² + 14x + 49 + x²
–> 2x² + 14x + 49 – 169 = 0
–> 2x² + 14x – 120 = 0
–> x² + 7x – 60 = 0
–> x² + 12x – 5x – 60 = 0
–> x (x +12) – 5(x +12) = 0
–> (x + 12) (x – 5) = 0
x = 5 or -12 (which is not possible)
∴ Required distance = 5 m
12) Answer: c)
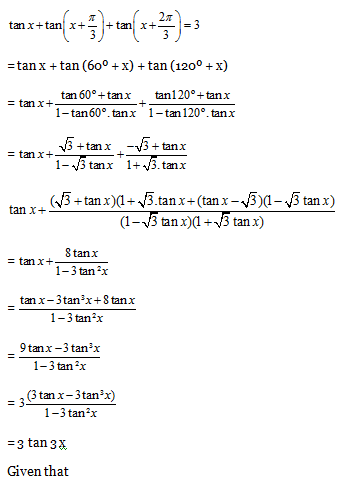
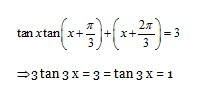
13) Answer: d)
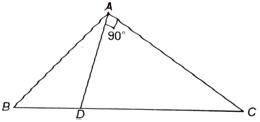
∆ADC is right-angled triangle with A = 90º/: ∆ ADC , ∠A = 90º
∴ AC² + AD² = CD²
In DABC/ DABC according to Apollonius Theorem
= 2 AD² + 2 BD² = AB² + AC²
= 2(CD² – AC²) + 2 BD² = AB² + AC²
BD = CD
∴ BD² = CD² =
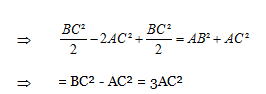
14) Answer: d)
As all of them have the same base so they have the same radius.
Suppose their radius is r and height is h.
∴ Curved surface area of hemisphere = 2pr² and curved surface area of the cone
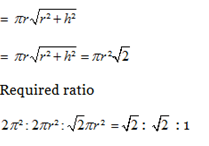
15) Answer :d)
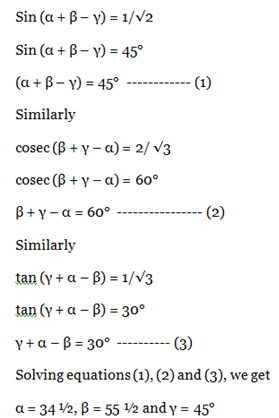
*******************
Click Here for More Quizzes
SSC Quantitative Aptitude Practice Questions (Day-7)
SSC Quantitative Aptitude Practice Questions (Day-6)
SSC Quantitative Aptitude Practice Questions (Day-5)





