SSC CGL EXAMS 2018 | Quantitative Aptitude Practice Questions (Day-13)

Dear Aspirants, Here we have given the Important SSC Exam 2018 Practice Test Papers. Candidates those who are preparing for SSC 2018 can practice these questions to get more confidence to Crack SSC 2018 Examination.

[WpProQuiz 4589]

Click here to view Quantitative Aptitude Questions in Hindi

1) sin θ – cos θ = √2cos θ, then find the value of sin θ + cos θ?

a) √2 sin θ

b) 2 sin θ cos θ

c) √2 sin² θ

d) √2 sin θ cos θ

2) What percentage of numbers is there from 1 to 75 has 1 or 6 in the unit’s digits?

a) 25%

b) 20%

c) 50%

d) 33.33%

3) A Man’s age is thrice as much of his son and twice as much of his wife. Average age of this family is 22. What is the sum of ages of his wife and son?

a) 36 years

b) 66 years

c) 30 years

d) 25 years

4) Find the number of diagonals of 8 side closed figure?

a) 22

b) 16

c) 20

d) 25

5) In a triangle PQR, O is an in center of ∆PQR. If ∠P = 60⁰. Find the ∠QOR.

a) 110⁰

b) 100⁰

c) 120⁰

d) 90⁰

6) P is completed a job in 8 hrs in a day. The same job is completed by R in 6 hrs a day. They are working together, how long the work will be completed?

a) 3 (1/7) hours

b) 3 (4/7) hours

c) 3 (3/7) hours

d) 3 (2/5) hours

7) The lengths of two parallel sides of a trapezium are 28 cm and 12 cm. If its height is 15 cm, then what is the area of trapezium?

a) 540 cm²

b) 300 cm²

c) 250 cm²

d) 350 cm²

8) Find m if the ordinate and abscissa of the point (6m, m² + 5m – 12) are equal

a) – 2 or 3

b) 2 or 3

c) – 3 or 4

d) 3 or – 4

9) The curved surface area of a cylindrical pillar is 660 m² and its volume 2310 m³. Find the height of the cylinder

a) 11 m

b) 15 m

c) 7 m

d) 8 m

10) When 15% of fruits were rotten, a seller remains some fruits unsold after 60 fruits were sold. On another day if only 10% of fruits were rotten, he can sale 65 fruits with same number of unsold fruits on previous day. How many fruits actually he has daily if he has same number of fruits on each day?

a) 100

b) 150

c) 300

d) 250

Answers :

1) Answer: a)

Sin θ – cos θ = √2cos θ

Squaring both side,

(sin θ – cos θ)² = 2cos² θ

sin² θ +cos² θ – 2 sin θ cos θ = 2 cos²θ

sin² θ = cos² θ + 2 sin θ.cos θ

Add Sin² θ on both sides

2 sin² θ = sin² θ +cos² + 2sin θ cos θ

2 sin² θ = (sin θ + cos θ) ²

sin θ + cos θ = √2 sin θ

2) Answer: b)

The Number which have 1 or 6 in unit’s digits are 1, 11, 21, 31, 41, 51, 61, 71, 6, 16, 26, 36, 46, 56, 66.

Total number with unit’s digit as 1 or 6 = 15

Total number = 75

Required percentage = (15*100)/ 75 = 20%

3) Answer:  c)

Man       :        His son

3          :            1

Man       :        His wife

2           :           1

Man       :        Wife      :       Son

6           :         3        :        2

Average age of this family = 22

Total age of this family = 22*3 = 66

6x + 3x+ 2x = 66 => 11x = 66

X = 6

Sum of ages of wife and son = 3x + 2x = 5x = 5 * 6 = 30 years

4) Answer:  c)

No. of diagonals of polygon = n (n – 3)/2 = 8 (8 – 3) / 2 = (8 * 5) /2 = 20

5) Answer: c)

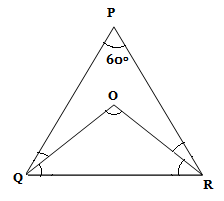
The angle made by any side with the in centre = 90° + half the opposite angle.

= 90° + ∠P/2

= 90⁰ + ½ *60⁰ = 90° + 30° = 120⁰

6) Answer: c)

P = 1/8 hours

R = 1/6 Hours

P + R = 1/8 + 1/6 = 7/24

= 3 (3/7) hours

7) Answer:  b)

Area of Trapezium = Half of sum of two parallel Sides * Heights

= (½)* [(s₁+s₂) * H]

= (28 + 12) /2 * 15 = 300 cm²

8) Answer:  c)

The ordinate of the point is m² + 5m – 12

Abscissa = 6m

6m = m² + 5m – 12

m² + 5m – 6m – 12 = 0

m² – m – 12 = 0

m² – 4m + 3m – 12 = 0

m (m – 4) + 3 (m – 4) = 0

m = – 3

m = 4

9) Answer: b)

Curved surface area of the cylinder= 2πrh = 660 m²

Volume of the cylinder = πr²h = 2310 m³

(πr² h)/(2πrh )= (2310 )/(660 )

R = 7

Curved surface area of the cylinder= 2πrh = 660 m²

= 2* 22/7 * 7 * h = 660 m²

= > h = 15 m

10) Answer: a)

Total Fruits = x

According to the question, unsold fruits were remain same

(x – 15x/100 – 60) = (x – 10x/100 – 65)

15x/100 + 60 = 10x/100 + 65

15% of x – 10 % of x = 65 – 60

5x/100 = 5

5x = 500

X = 100

Total number of fruits = 100

*******************

Click Here for More Quizzes

SSC CGL EXAMS 2018 |Quantitative Aptitude Practice Questions (Day-12) 

SSC CGL EXAMS 2018 |Quantitative Aptitude Practice Questions (Day-11) 

SSC CGL EXAMS 2018 | Quantitative Aptitude Practice Questions (Day-10)