Dear Aspirants, Here we have given the Important SSC Exam 2018 Practice Test Papers. Candidates those who are preparing for SSC 2019 can practice these questions to get more confidence to Crack SSC 2019 Examination.
[WpProQuiz 4963]
Click Here for SSC CGL Online Mock TestÂ
 Click here to view Quantitative Aptitude Questions in Hindi
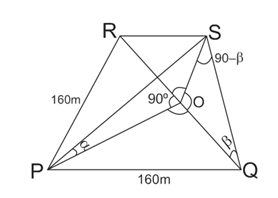
1) PQR is a triangular park with PQ = PR= 160 meter. A clock tower is situated at the mid-point of QR. The angles of elevation of the top of the tower at P & Q are Cot–1 3.2 and cosec–12.6 respectively. The height of the tower is—
a) 50 meters
b) 30 meters
c) 60 meters
d) 40 meters
2) If a, b, c, d and e are positive real numbers such that a + b + c + d + e = 30, find the maximum value of a3 b3 c6 d2 e2.
a) 225. 324
b) 224.325
c) (–6)24
d) (6)25
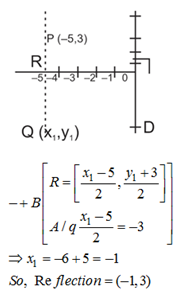
3) What is the reflection of the point (– 5, 3) in the line x = – 3?
a) (–2, 3)
b) (–1, 3)
c) (– 1, – 3)
d) –2, – 3
4) Two sides of a triangle are √5 – 1 & √5 + 1 units and their included angle is 60o, Solve the triangle and find the value of ‘a’?
a) √3
b) √2
c) √6
d) 2√3
5) Find the remainder of 92426/70
a) 11
b) 12
c) 9
d) 61
6) Find the last two digit of (333333)164
a) 71
b) 61
c) 51
d) 41
7) If N = a7b625, and N is divisible by 11 then how many possible pairs of values of a and b?
a) 4
b) 3
c) 2
d) Cannot be determine
8) What is the least value of 3 sin2q + 3 cos2q + 4 tan2q + 4 cot2 q + 5 sec2 q + 5 cosec2q?
a) 12
b) 13
c) 21
d) 31
9) The length of the circumradius of a triangle having sides of lengths 16 cm, 20 cm & 24 cm is
a) 32/7
b) 32 /√7
c) 4/12 * 37/188
d) 32√7/9
10) If ax + by = 8, bx –ay =2 and x2 + y2 = 4
a) 17
b) 18
c) 19
d) 20
Answers :
1) Answer: d)
2) Answer: a)
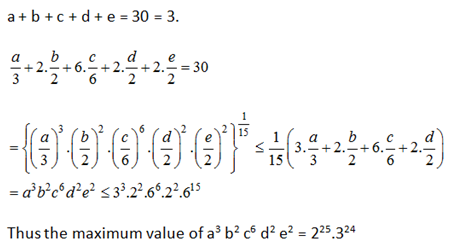
3) Answer:Â d)
4) Answer:Â Â c)
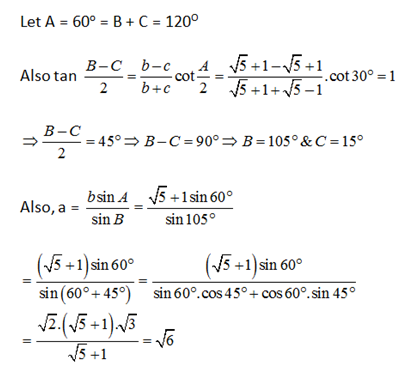
5) Answer: a)
6) Answer: b)
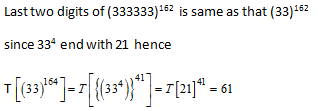
7) Answer: a)
If N is divisible by 11 then
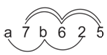
(a + b + 2) – (7 + 6 + 5) = 0 or 11, 22
a + b + 2 – 18 = 0, 11, 22,
a + b + 2 – 18 = 0, 11, 22
a + b = 16/161+11/16+22
16/27/38
a + b = 16 (possible)
a + b = 27 / 38 etc. (Not possible, because a and b single digit number and maximum of sum of a & b for single digit = 9 + 9 = 18 = a + b = 16
(9, 7) (7, 9) & (8, 8) (8, 8) only these pairs are possible.
8) Answer: d)
3 (sin2q + cos2q) + 4 tan2 q + 4 cot2 q + 5 sec2q + 5 cosec2q
= 3 + 4 tan2q + 4 cot2q + 5 (1 + tan2q) + 5 (1 + cot2 q)
=3 + 5 + 5 + (9 tan2q + 9 cot2q) min
= 13 + 2 √(9×9)
= 13 + 2 9 = 13 + 18 = 31
9) Answer:Â b)
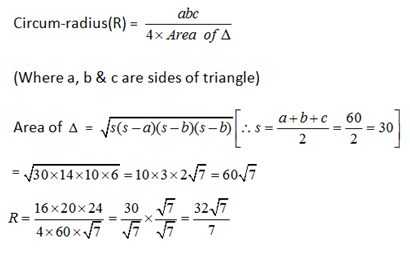
10) Answer:Â a)
Given
ax + by = 8……. (i)
bx – ay = 2 ……..(ii)
We squaring on both sides on both the equation and then add it.
(ax + by)2 + (bx – ay)2 = 64 + 4
a2x2 + b2y2 + b2x2 + a2y2 + 2abxy – 2abxy = 68
x2 (a2+b2) + y2 (a2 + b2) = 68
(a2 + b2) (x2 + y2) = 68
a2 + b2 = 68/4 = 17
*******************
Click Here for SSC CGL Online Mock TestÂ
Click Here for More Quizzes
SSC CGL EXAMS 2019 |Quantitative Aptitude Practice Questions (Day-22)Â
SSC CGL EXAMS 2019 |Quantitative Aptitude Practice Questions (Day-21)Â
SSC CGL EXAMS 2019 |Quantitative Aptitude Practice Questions (Day-20)Â
