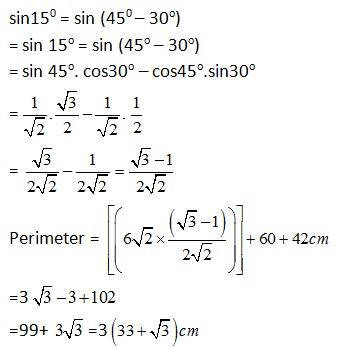Dear Aspirants, Here we have given the Important SSC Exam 2019 Practice Test Papers. Candidates those who are preparing for SSC 2019 can practice these questions to get more confidence to Crack SSC 2019 Examination.
[WpProQuiz 5170]
Click Here for SSC CGL Online Mock Test
Click here to view Quantitative Aptitude Questions in Hindi
1) Find the remainder of the following one?
![]()
a) 2
b) 3
c) 1
d) 0
2) Find the value of the unit digit of the given expression
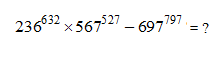
a) 1
b) 2
c) 4
d) 0
3) Find the minimum value of the given expression?
y =5x2 – 6 x + 7
a) 13/ 5
b) 5/ 13
c) –13 / 5
d) –5 / 13
4) The four angles M, N, O, P of a quadrilateral be in the ratio of 1 : 2 : 2 : 1. Find the value of
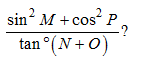
a) 1/√3
b) √3
c) 1/3
d) 3
5) The average of A, B & C is 62 the average of B, C, D & E is 58. The sum of A and D is 25. Then find the value A .M of all four terms A, B, C & D?
a) 30
b) 60
c) 50
d) 40
6) In an election there were 3 contestants in this election 10% people do not polled their vote of total number registered vote. 10% votes were declared invalid. The ratio between vote for winner, runner and 2nd runner is 4 : 3: 2 and winner won by 18000 vote by 2nd runner. Then find the total number of vote who got runner?
a) 271000
b) 36000
c) 42000
d) Cannot be determine
7) Total surface area of toy which is in shape of cone is 15400 (√3 + 1) cm2. The radius is 2√3 times to the (r), and then find its curved surface area?
a) 14000
b) 12600
c) 18900
d) 5400√3
8)
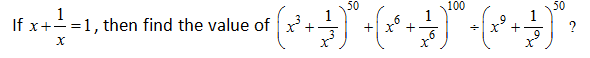
a) 1 – (–2)50
b) 1 + (–2)50
c) 1 + (2)50
d) 1 – (2)50
9) If x + y = 1, then find the maximum value of xy?
a) ½
b) ¼
c) 1
d) ∞
10) Find the perimeter of a ∆ whose base is 60 cm and one other side is 42cm and other third side is 6√2 times of sin 15°?
a) 3(33 + √3) cm
b) 6 (33 + √5) cm
c) 3(33 + √3) cm
d) None of these
Answers :
1) Answer: a)

2) Answer: d)
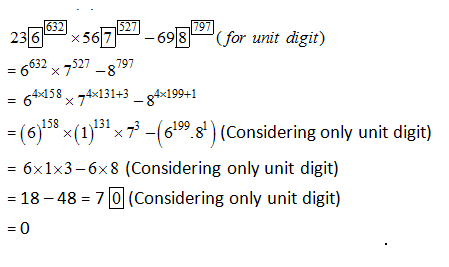
3) Answer: a)
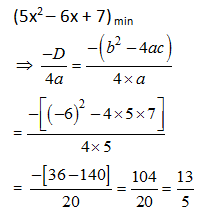
4) Answer: a)
X+ 2x + 2x + x = 360
6x = 3600
X = 600
Angles of M, N, O, P = 60, 120, 120, 60
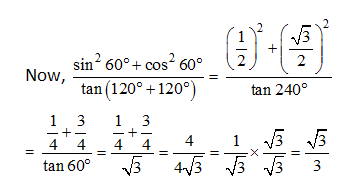
5) Answer: c)

6) Answer: a)
Let, Total Registered for vote = 100%
Total polled vote = 90%
Invalid vote = 10% of total polled vote.
= (90×10/100) = 9%
So, valid vote = 90% – 9% = 81%
Thereare three competitors as winner, runner and 2nd runner and their ratio of no of votes getting
4x + 3x + 2x =9x = 81%]
X = 9%
Winner gets 4 = 4 × 9 = 36%
Runner get 3 = 3 × 9 – 27 %
2ndrunner get 2 = 2 × 9 = 18%
2nd runner won by winner with 18,000 vote
(36% – 18%) => 18% = 18000
So, Runner gets => 27% = 27× 1000 = 27000
7) Answer: d)
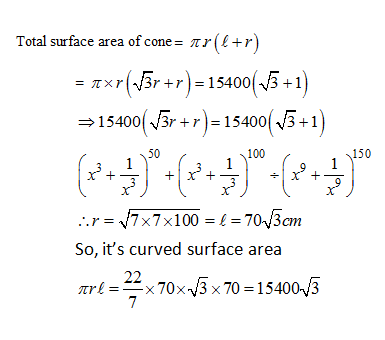
8) Answer: b)
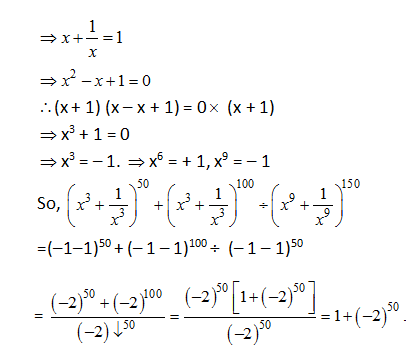
9) Answer: b)
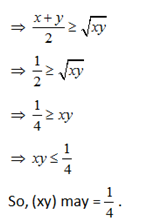
10) Answer : a)