Dear Aspirants, Here we have given the Important SSC Exam 2018 Practice Test Questions. Candidates those who are preparing for SSC 2018 can practice these questions to get more confidence to Crack SSC 2018 Examination.
[WpProQuiz 4499]Click here to view Quantitative Aptitude Questions in English
दिशानिर्देश: प्रश्न(1-4): दिया गया बार ग्राफएक फर्म की आय इंगित करता है
ग्राफ का अध्ययन करें और प्रश्न का उत्तर दें-
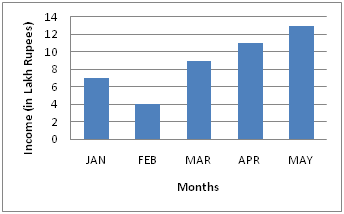
1) कौन सी अवधि आय की स्थिर वृद्धि दर्शाती है?
(a) मार्च से मई
(b) फ़रवरी से अप्रैल
(c) फ़रवरी से मई
(d) अनुमान लगाने के लिए आंकड़े अधूरे हैं
2) किस महीने के दौरान, आय का अनुपात पिछले महीने सबसे बड़ा है?
(a) फ़रवरी
(b) मार्च
(c) अप्रैल
(d) मई
3) मई में आय फ़रवरी से कितना गुना है?
(a) 3.25
(b) 4
(c) 3.5
(d) 5
4) फर्म की औसत मासिक आय (लाख रुपये में) है:
(a) 7.6
(b) 6
(c) 8
(d) इनमे से कोई नहीं
5) एक वस्तु का मूल्य 65 रुपये अंकित है। एक ग्राहक ने 56.16 रुपये में इस वस्तु को खरीदा और दो लगातार छूट मिली जिनमें से पहला 10% है। दुकानदार द्वारा दी गई दूसरी छूट की दर क्या थी
(a) 3%
(b) 4%
(c) 6%
(d) 2%
6) यदि एक मूलधन P 2 साल में Q बन जाता है जब ब्याज R % अर्ध-वार्षिक होता है। और यदि वही मूलधन P 2 साल में Q बन जाता है जब ब्याज S % सालाना होता है, तो निम्न में से कौन सा सत्य है?
(a) R > S
(b) R = S
(c) R < S
(d) R < D
7) 60 किलो मिश्र धातु A को 100 किलोग्राम मिश्र धातु B के साथ मिश्रित किया जाता है। यदि मिश्र धातु A का अनुपात 3: 2 में होता है और इसमें टिन और ताम्बा होता है और मिश्र धातु B में अनुपात 1: 4 में टिन और तांबा होता है, तो नए मिश्र धातु में टिन की मात्रा है
(a) 36 किलोग्राम
(b) 44 किलोग्राम
(c) 53 किलोग्राम
(d) 80 किलोग्राम
8) यदि और, तोहै
(a) 0
(b) 2
(c) 1
(d) 3
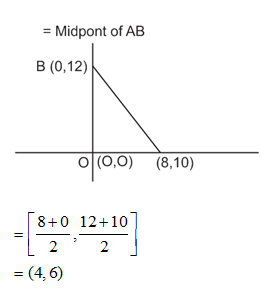
9) Δ O ABके शिखरऔर O (O, O), A (8, 0) and B (0, 12)हैं। Δ OAB के परिवृत्त ज्ञात कीजिये
(a) (8, 10)
(b) (4, 6)
(c) (3, 5)
(d) इनमे से कोई नहीं
10) यदि α और β समीकरण x² + 6x + 1 = 0 के मूल हैं, तब | α – β | का मान ज्ञात कीजिये?
(a) 6
(b) 3√2
(c) 4√2
(d) 12
11) सभी दो अंकों की सम संख्याओं का योग उनमें से किसी एक से छोड़कर विभाजित किया जाता है जो शेषफल नहीं बचता है। यह ज्ञात है कि अंकों का योग 9 का भाजक है, और यह कि शेषफल और भाजक में अंक एक दूसरे के विपरीत हैं। भाजक का क्या मान है
(a) 18
(b) 36
(c) 54
(d) 72
12) का न्यूनतम मान ज्ञात करें
(a) 2
(b) 2(3-1/√2 )
(c) 3i-1/√2
(d) इनमे से कोई नहीं
13) 30 के सभी गुणनखंड का गुणांक ज्ञात कीजिये।
a) 243454
b) 243455
c) 243654
d) 233454
14) चार अंकों का सबसे छोटटी संख्या क्या है जो किसी भी इकाई अंक अभाज्य संख्याओं द्वारा विभाजित होने पर समान शेषफल देता है
(a) 1051
(b) 1034
(c) 2065
(d) इनमे से कोई नहीं
15) राहुल की बाल्टी के वृत्तिय सिरों की त्रिज्या 28 सेंटीमीटर ऊंची है और राहुल की बाल्टी की क्षमता12 सेंटीमीटर हैं
(a) 12684 सेमी3
(b) 1683 सेमी3
(c) 18095 सेमी3
(d) 20064 सेमी3
Answers :
1) उत्तर:(a)
यह ग्राफ द्वारा साफ़ पता चलता है कि आय में वृद्धि
मार्च से मई में है।
2) उत्तर:(b)
मार्च महीने का अनुपात फरवरी से अधिक है
3) उत्तर:(a)
![]()
4) उत्तर(d)
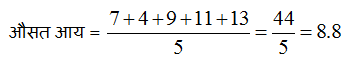
5) उत्तर(b)
पहली छूट के बाद वस्तु की कीमत
65 – 6.5 = 58.5 रुपये
इसलिए, दूसरी छूट
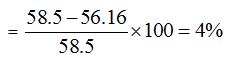
6) उत्तर:(c)
चूंकि ब्याज प्रति वर्ष R % पर अर्ध वार्षिक रूप से एकत्रित किया जाता है, इसलिए मूल्य RS के मूल्य से कम होगा (याद रखें, अर्ध वार्षिक कंपाउंडिंग हमेशा जमाकर्ता के लिए लाभदायक है)
7) उत्तर: (b)
60 किलो A में टिन की मात्रा = 24 किलो
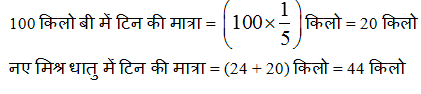
8) उत्तर:(a)
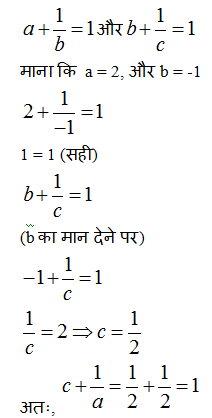
9) उत्तर: (b)
दिया है,OAB एक सम कोणत्रिभुज है और सम कोण के परिवृत्तकर्ण का मध्यबिंदु है।
10) उत्तर:(c)
α और β समीकरण x² + 6x + 1 = 0 के मूल हैं
∴ α और β = − 6 & αβ = 1
अब, (α – β) 2 = (α + β) 2 – 4 αβ
= (-6)² – 4
= 36 – 4 = 3
![]()
11) उत्तर(c)
सभी दो अंकों की सम संख्या का योग
= 10 + 12 + 14 + …. + 98
= 2(5 + 6 + 7 + …. + 49)
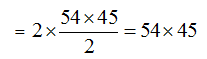
विभाजक 18, 36 या 54 होना चाहिए क्योंकि यह उनमें से एक है। यह 54 होना चाहिए जब 54 × 4, 54 से विभाजित होता है, तो मात्रा 45 है और इन में, अंकों को उलट दिया जाता है। तो, विभाजक54 होना चाहिए
12) उत्तर:(d)
हम जानते हैं कि
AM (a, b) > GM (a, b)
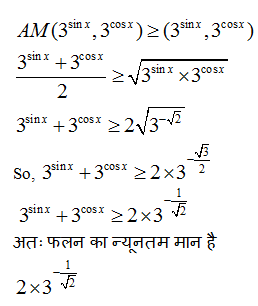
13) उत्तर :(a)
विधि I.
माना कि हम 30 के सभी कारकों को सूचीबद्ध करेंगे, ये हैं-
1,2, 3, 5, 6, 10, 15, 30
अब हम इन सभी गुणनखंड कोअभाज्यगुणनखंड बनाने के रूप में लिखेंगे
(2o 3o 5o) (21) (31) (51) (2131) (2151) (3151)
= (21+1+1+1) (31+1+1+1) (51+1+1+1)
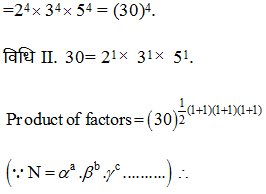
N के गुणनखंड के गुणांक = 304.
=(N) 1/2 (a+1) (b+1)(c+1)x……….
14) उत्तर : (a)
एक अंक के प्राइम नंबर 2, 3, 5 और 7 हैं। उनमें से सबसे छोटा है 2।
–> यह केवल ओ और 1 को रहने वालों के रूप में देता है। इसलिए संभावित संख्या के (के 2, 3, 5 और 7) के एलसीएम + 1 या 210 के + 1 के रूप में होना चाहिए। इसलिए, केवल इस विकल्प में विकल्प (1) है।
15) उत्तर: (d)

*****************************
Click here for More Quizzes
SSC CGL EXAMS 2018 | Quantitative Aptitude Questions Hindi (Day-8)
SSC CGL EXAMS 2018 | Quantitative Aptitude Questions Hindi (Day-7)
SSC CGL EXAMS 2018 | Quantitative Aptitude Questions Hindi (Day-6)