Dear Aspirants, you can find the Quantitative Aptitude questions with detailed explanations for the SSC exams. Nowadays the competitive level of the exam has been increasing consistently. Due to the great demand for the government job, the level of the toughness reached greater. Candidates have to enhance the preparation process in order to drive in the right path. It doesn’t need to clear the prescribed cutoff. You must have to score good marks more than the cut off marks to get into the final provisional list. Here we have updating the Quantitative Aptitude questions with detailed explanations on a daily basis. You can practice with us and measure your level of preparation. According to that you can sculpt yourself in a proper way. SSC aspirants kindly make use of it and grab your success in your career.
1) If x + y = 4, then what is the value of x3 + y3 + 12xy?
(a) 16
(b) 32
(c) 64
(d) 256
2)
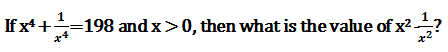
(a) 14
(b) 2√7
(c) 10√2
(d) 10
3) If 3x – [1/(3x)] = 9, then what is the value of x2 + [1/(81x2)]?
(a) 7
(b) 83/9
(c) 11
(d) 121/9
4) If x3 – y3 = 112 and x – y = 4, then what is the value of x2 + y2?
(a) 16
(b) 20
(c) 24
(d) 28
5)

(a) 625
(b) 3125
(c) 2525
(d) 2500
6) In ΔABC, ∠A : ∠B : ∠C = 3 : 3 : 4. A line parallel to BC is drawn which touches AB and AC at P and Q respectively. What is the value of ∠AQP – ∠APQ?
(a) 12
(b) 18
(c) 24
(d) 36
7) In the given figure, O is the center of the circle, ∠CAO = 35o and ∠CBO = 45o. What is the value (in degrees) of ∠AOB?
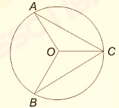
(a) 90
(b) 110
(c) 160
(d) 130
8) In the given figure, PQRis drawn such that PQ is tangent to a circle whose radius is 10 cm and QR passes through centre of the circle. Point R lies on the circle. If QR = 36 cm, then what is the area
(in cm2) of PQR?
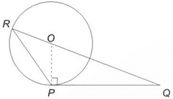
(a) 134.5
(b) 148
(c) 166.15
(d) 180
9) The side QR of ΔPQR is produced to S. If ∠PRS = 105° and ∠Q = (1/2)∠P, then what is the value of ∠P?
(a) 45
(b) 60
(c) 70
(d) 75
10) The perimeter of an isosceles triangle is 64 cm and each of the equal sides is 5/6 times the base. What is the area (in cm2) of the triangle?
(a) 169
(b) 192
(c) 196
(d) 184
Answers :
1) Answer: C
x³ + y³ + 12xy = (x + y) (x2 + y² – xy) + 12xy
= (x + y) [(x + y)² – 3xy] + 12xy
= 4 [16 – 3xy] + 12xy
= 64 – 12xy + 12xy = 64
2) Answer: A
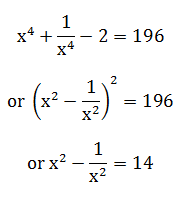
3) Answer: B
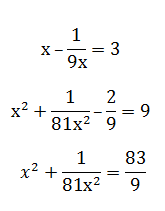
4) Answer: C
x³ – y³ = 112 x – y = 4
112 = 4 (x² + y² + xy) …(i)
or 112 = 4 [(x – y)² + 3xy]
or 28 = [16 + 3xy]
or 4 = xy
& from (i)
28 = x² + y² + 4
⇒ x² + y² = 24
5) Answer: C
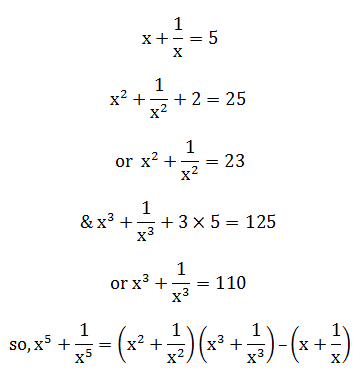
= 23 × 110 – 5
= 2530 – 5
= 2525
6) Answer: B
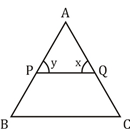
x – y = ?
3a + 3a + 4a = 180°
⇒ 10a = 180°
or a = 18°
So,
x – y = ∠C – ∠B
= (4 – 3) a
= 18°
7) Answer: C
Clearly ∆ AOC & ∆BOC are isosceles ∆
∴ ∠OAC = ∠OCA
= 35°
⇒ ∠AOC = 180 – 2 × 35°
= 110
& ∠CBO = ∠OCB = 45°
⇒ ∠BOC = 180 – 2 × 45°
= 90°
so, ∠AOB = 90° + 110° = 200°
or 360° – 200 = 160°
8) Answer: C
Clearly, ∆POQ is right angled at P.
& OQ = 36 – 10 = 26
& OP = 10
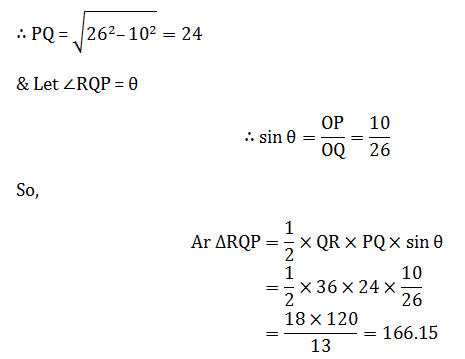
9) Answer: C
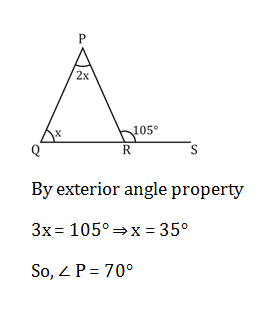
10) Answer: B
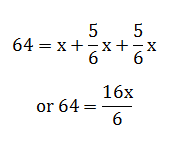
or x = 24
∴ sides are 20, 20, 24
So, S = 32
∴ ∆Ar = √(32 × 12 × 12 × 8)
= 8 × 4 × 3 × 2
= 192 cm²
| Check Here to View SSC CGL / CHSL 2021 Quantitative Aptitude Questions | ||
| Day – 56 | Day – 55 | Day – 54 |





