Dear Aspirants, you can find the Quantitative Aptitude questions with detailed explanations for the SSC exams. Nowadays the competitive level of the exam has been increasing consistently. Due to the great demand for the government job, the level of the toughness reached greater. Candidates have to enhance the preparation process in order to drive in the right path. It doesn’t need to clear the prescribed cutoff. You must have to score good marks more than the cut off marks to get into the final provisional list. Here we have updating the Quantitative Aptitude questions with detailed explanations on a daily basis. You can practice with us and measure your level of preparation. According to that you can sculpt yourself in a proper way. SSC aspirants kindly make use of it and grab your success in your career.
1) If interest being compound half yearly then what sum (in Rs) will amount to Rs 38416 in 2 years at the rate of 80% per annum at compound interest?
(a) 14000
(b) 15000
(c) 10000
(d) 12000
Direction (2-5): The table given below shows the number of students studying in five colleges in the given five years.
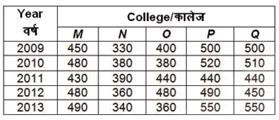
2) If in year 2011, in college N, 80% of the total students appeared in a exam, out of which 50% students passed, then how many students passed the exam?
(a) 136
(b) 152
(c) 156
(d) 162
3) What is the ratio of the total number of students of college N in all years to the total number of students of all the colleges styding in the year 2011?
(a)100 : 107
(b) 90 : 107
(c) 90 : 119
(d) 90 : 127
4) What is the average of the total number of students studying in college M in the given years?
(a) 412
(b) 420
(c) 400
(d) 466
5) In which of the given years the average number of students studying is maximum?
(a) 2011
(b) 2009
(c) 2010
(d) 2013
6) The perimeter of a rhombus in 20 cm and one of the diagonal is 8 cm. what is the area (in cm2) of the rhombus?
(a) 12
(b) 24
(c) 48
(d) 96
7) Three circles of radius 9 cm are kept touching each other. The string is tightly tied around the three circles. What is the length (in cm) of the string?
(a) 48 + 18π
(b) 48 + 24π
(c) 54 + 18π
(d) 54 + 24π
8) The difference between circumference and the radius of a circle is 111 cm. What is the area (in cm2) of the circle?
(a) 469
(b) 1386
(c) 912
(d) 1086
9) If the diameter of a sphere is 14 cm, then what is the curved surface area (in cm2) of the sphere?
(a) 616
(b) 1232
(c) 2464
(d) 576
10) If the ratio of volume of two cubes is 11: 13, then what is the ratio of the sides of the two cubes?
(a) 11 : 13
(b) 121 : 169
(c) (11)1/2 : (13)1/2
(d) (11)1/3 : (13)1/3
Answers :
1) Answer: C
let the original sum = 100
For 1 yr = 40 + 40 + (40 × 40) / 100
= 96%
For 2 yrs = 96 + 96 + (96 × 96)/100
= 192 + 92.16
= 284.16%
Total sum after two years = 100 + 284.16 =384.16%
2) Answer: C
= ½ × 80/100 × 390
= 0.4 × 390
= 156
3) Answer: B
Ntotal=1800
No. of students in year 2011 ⇒ 2140
Ratio = 1800 : 2140
90: 107
4) Answer: D
MTotal=2330/5 = 466
5) Answer: D
Total students in year
2009 ⇒ 2180
2010 ⇒2270
2011 ⇒2140
2012 ⇒2260
2013 ⇒2290
Hence average no. of students was maximum in 2013.
6) Answer: B
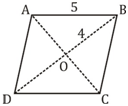
∵ diagonal of rhombus intersect at right angle hence
AO = 3 cm ⇒ AC = 6 cm
Area of rhombus = ½ ×6 × 8 = 24 cm
7) Answer: C
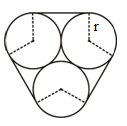
Curved string = 2πr
= 18π cm
Straight string = 3 × (28) = 54 cm
Total length of string = 54 + 18π cm
8) Answer: B
(2π – 1) r = 111
(44/7–1) r = 111
37/7 r = 111
r = 21 cm
Area of circle = 22/7 × 21 × 21
=1386 cm2
9) Answer: A
d = 14 cm
r = 7 cm
C.S.A. of a sphere = 4πr²
= 4 × 22/7 × 7 × 7
= 616 cm2
10) Answer: D
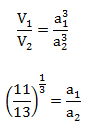
| Check Here to View SSC CGL / CHSL 2021 Quantitative Aptitude Questions | ||
| Day – 70 | Day – 69 | Day – 68 |





