Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for SBI Clerk Prelims 2020 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Ensure Your Ability Before the Exam – Take SBI Clerk 2020 Prelims Free Mock Test
Data Interpretation
Directions (1 – 5): Study the following information carefully and answer the questions given below?
The given line graph shows the number of words typed in the book by six different persons in one hour.
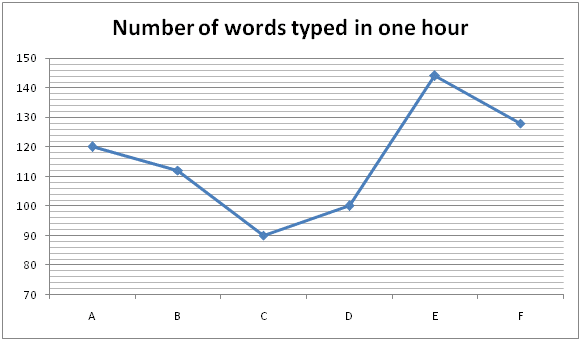
1) What is the total time required to completely type 200 words for each A and D?
a) 5 hours 40 minutes
b) 2 hours 40 minutes
c) 3 hours 40 minutes
d) 4 hours 40 minutes
e) None of these
2) If G can type 150 words in one hour, find the average of words both G and A together can type in 15 hours?
a) 5280
b) 5180
c) 5380
d) 5080
e) None of these
3) If the ratio of the efficiency of B to G is 4: 5 and the ratio of the efficiency of D to H is 5: 7, how many words typed by G and H in 330 minutes?
a) 1240
b) 1460
c) 1380
d) 1540
e) None of these
4) If A decreased his efficiency by 20%, F increased his efficiency by 25% and D increased the efficiency by 30%, how many words typed by A, B, C, D, E and F together in 4 hours?
a) 2928
b) 2945
c) 2944
d) 2956
e) None of these
5) In how much time will required F and B together to type 1800 words in the book?
a) 380 minutes
b) 400 minutes
c) 420 minutes
d) 450 minutes
e) 360 minutes
Quadratic equation
Directions (6 – 10): In each of the following questions, two equations are given. You have to solve both the equations to find the relation between x and y and give answer as,
a) If x < y
b) If x > y
c) If x ≤ y
d) If x ≥ y
e) If x = y or relationship between x and y cannot be determined
6) I) 5x2 – 22x + 21 = 0
II) 2y2 – 13y + 21 = 0
7) I) 2x2 – 17x + 36 = 0
II) 6y2 – 49y + 99 = 0
8) I) 30x2 + 162x + 216 = 0
II) 3y2 + 19y + 30 = 0
9) I) 2x2 – 7x + 5 = 0
II) 2y2 – 54y + 364 = 0
10) I) x2 – 29x + 210 = 0
II) 8y2 – 49y + 45 = 0
Answers :
Directions (1 – 5):
1) Answer: C
120 words typed by A = 1 hour
Time required for A to type one word = 1/120
Time required for A to type 200 word = 200/120
Time required for D to type one word = 1/100
Time required for D to type 200 word = 200/100
Total time = 200/120 + 2 = 440/120
= 11/3
= 3 hours 40 minutes
2) Answer: E
G types the number of words in given book in one hour = 150
A types the number of words one hour = 120
Required average = 15 * (120 + 150)/2 = 2025
3) Answer: D
G types the number of words in book in one hour = 5/4 * 112 = 140
H types the number of words in book in one hour = 7/5 * 100 = 140
Required words = (140 + 140) * 5.5 = 1540
4) Answer: A
A = 80/100 * 120 = 96
B = 112
C = 90
D = 130/100 * 100 = 130
E = 144
F = 125/100 * 128 = 160
Required number of words = (96 + 112 + 90 + 130 + 144 + 160) * 4 = 2928
5) Answer: D
F and B together can type the number of word in one hour = 112 + 128 = 240
Required time = 1800 * 1/240 = 7.5 hours
Directions (6 – 10):
6) Answer: C
From I =>
5x2 – 22x + 21 = 0
=> 5x(x – 3) – 7(x – 3) = 0
=> (5x – 7) (x – 3) = 0
=> x = 7/5, 3
From II =>
2y2 – 13y + 21 = 0
=> 2y(y – 3) – 7(y – 3) = 0
=> (2y – 7) (y – 3) = 0
=> y = 7/2, 3
Hence, x ≤ y
7) Answer: E
From I =>
2x2 – 17x + 36 = 0
=> 2x(x – 4) – 9(x – 4) = 0
=> (2x – 9) (x – 4) = 0
=> x = 9/2, 4
From II =>
6y2 – 49y + 99 = 0
=> 3y (2y – 9) – 11(2y – 9) = 0
=> (3y – 11) (2y – 9) = 0
=> y = 11/3, 9/2
Hence, relationship between x and y cannot be determined.
8) Answer: D
From I =>
30x2 + 162x + 216 = 0
=> 30x(x + 3) + 72(x + 3) = 0
=> (30x + 72) (x + 3) = 0
=> x = -3, -2.4
From II =>
3y2 + 19y + 30 = 0
=> 3y(y + 3) + 10(y + 3) = 0
=> (3y + 10) (y + 3) = 0
=> y = -3, -3.33
Hence, x ≥ y
9) Answer: A
From I =>
2x2 – 7x + 5 = 0
=> 2x (x – 1) – 5 (x – 1) = 0
=> (2x – 5) (x – 1) = 0
=> x = 2.5, 1
From II =>
2y2 – 54y + 364 = 0
=> 2y(y – 13) – 28(y – 13) = 0
=> (2y – 28) (y – 13) = 0
=> y = 13, 14
Hence, x < y
10) Answer: B
From I =>
x2 – 29x + 210 = 0
=> x (x – 14) – 15(x – 14) = 0
=> (x – 15) ( x – 14) = 0
=> x = 14, 15
From II =>
8y2 – 49y + 45 = 0
=> 8y (y – 5) – 9 (y – 5) = 0
=> (8y – 9) (y – 5) = 0
=> y = 5, 9/8
Hence, x > y
| Check Here to View SBI Clerk Prelims 2020 Quantitative Aptitude Questions | ||
| Day 37 | Day 36 | Day 35 |
| Click Here for SBI Clerk 2020 – Detailed Exam Notification | ||





