Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for SBI Clerk Mains 2020 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Ensure Your Ability Before the Exam – Take SBI Clerk 2020 Mains Free Mock Test
Quadratic equation
Directions (1 – 5): In the following questions, two equations I and II are given. You have to solve both equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established.
1) I) x2 – 40x + 391 = 0
II) y2 – 8y – 345 = 0
2) I) 2x2 + 28x + 98 = 0
II) y2 + 20y + 91 = 0
3) I) 3x2 – 12x – 135 = 0
II) y2 – 19y + 90 = 0
4) I) x2 + 42x + 405=0
II) y2 + 45y + 506=0
5) I) x2 – 21x + 108 = 0
II) y2 – 27y + 176 = 0
Data Interpretation
Direction (6 – 10): Study the following information carefully and answer the given questions?
Relationship cannot be established between x and y.
The given bar graph shows the percentage increment in the number of students on 2014 from 2013 and 2015 from 2014 in 5 different colleges A, B, C, D and E.
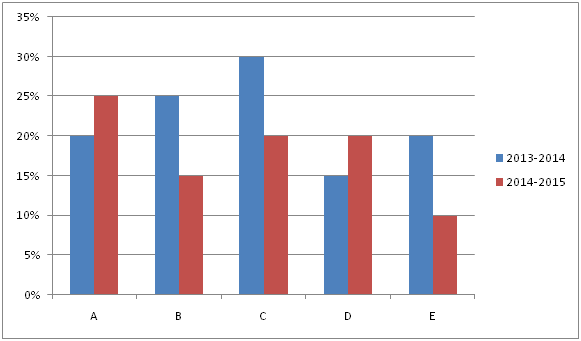
6) Find the total number of girl students from college A in 2013?
Statement I: Ratio of the number of boys to girls in college A in 2015 is 4:5 and the number of boys from A in 2013 is 80% of the number of boys from A in 2015.
Statement II: The number of girls from A in 2015 is 300.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
7) What is the total number of students from B in 2013?
Statement I: If the number of girl students from B in 2013, 2014 and 2015 is 60%, 50% and 45% respectively and the average number of boys from B in 2013, 2014 and 2015 is 581.
Statement II: Difference between the total number of students from B in 2014 and 2015 is 480.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
8) If sum of the total students from C in 2013 and 2015 is 640.
Quantity I: Ratio of the number of boys to girls from C in 2014 is 2: 3 and the total number of boy students from C in 2015 is 60% of the total number of girls from C in 2014. Find the total number of girls from C in 2015?
Quantity II: Ratio of the girls to boys from C in 2013 is 2: 3 and the ratio of the number of boys from C in 2014 to the number of girls from C in 2013 is 7: 5. What is the total number of girls from C in 2014?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
9) What is the average number of students from E in 2015 and 2013?
Statement I: Ratio of the number of boys from E in 2013, 2014 and 2015 is 2: 4:5 and the ratio of the girls from E in 2013, 2014 and 2015 is 3: 4: 2.
Statement II: Difference between the number of girls from E in 2014 and the number of boys from E in 2015 is 120.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
10) Find the average number of girls from D in 2013, 2014 and 2015 together?
Statement I: Total number of students in 2013 from D is 200 more than that the number of students in 2013 from E. Ratio of the number of girls to boys from D in 2013 is 3:2.
Statement II: Ratio of the number of boys to girls from D from in 2014 is 5:7 and the number of girl students from D in 2015 is 90.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
Answers :
Directions (1 – 5):
1) Answer: E
I) x2 – 40x + 391 = 0
(x – 17) (x – 23) = 0
x = 17, 23
II) y2 – 8y – 345 = 0
(y + 15) (y – 23) = 0
y = -15, 23
Relationship can’t be determined.
2) Answer: B
I) 2x2 + 28x + 98 = 0
2x2 + 14x + 14x + 98 = 0
2x(x + 7) + 14(x + 7) = 0
(2x + 14)(x + 7) = 0
x = -7, -7
II) y2 + 20y + 91 = 0
(y + 7) (y + 13) = 0
x = -7, -13
x ≥ y
3) Answer: D
I) 3x2 – 12x – 135 = 0
3x2 – 27x + 15x – 135 = 0
3x(x – 9) + 15(x – 9) = 0
(3x + 15)(x – 9) = 0
x = -5, 9
II) y2 – 19y + 90 = 0
(y – 10) (y – 9) = 0
y = 10, 9
x ≤ y
4) Answer: E
I) x2 + 42x + 405=0
(x + 15) (x + 27)=0
x = -15, -27
II) y2 + 45y + 506 = 0
(y + 22) (y + 23) = 0
y = -22, -23
Relationship cannot be established between x and y.
5) Answer: E
I) x2 – 21x + 108 = 0
(x – 9) (x – 12) = 0
x = 9, 12
II) y2 – 27y + 176 = 0
(y – 16) (y – 11) = 0
y = 16, 11
Relationship cannot be established between x and y.
Directions (6 – 10):
6) Answer: D
From statement I,
Total number of students from A in 2015 = 9x
Number of boys from A in 2015 = 4x
Number of girls from A in 2015 = 5x
Number of boys from A in 2013 = 80/100 * 4x = 16x/5
So, Statement I alone is not sufficient to answer the question.
From statement II,
Number of girls from A in 2015 = 300
So, Statement II alone is not sufficient to answer the question.
From I and II,
Number boys from A in 2015=4/5 * 300 = 240
Total number of students from A in 2015 = 9/5 * 300 = 540
Total number of students from A in 2013 = 540 * 100/125 * 100/120
= 360
Number of boys from A in 2013 = 80/100 * 240 = 192
Number of girls from A in 2013 = 360 – 192 = 168
7) Answer: C
From statement I,
Total number of students from B in 2013 = x
Total number of students from B in 2014 = 125x/100 = 5x/4
Total number of students from B in 2015 = 5x/4 * 115/100 = 23x/16
Number of boys from B in 2013 = x * 40/100 = 2x/5
Number of boys from B in 2014 = 5x/4 * 50/100 = 5x/8
Number of boys from B in 2015 = 55/100 * 23x/16 = 253x/320
Average of boys = 581
(2x/5 + 5x/8 + 253x/320) / 3 = 581
(128x + 200x + 253x/320) = 1743
x = 960
Total number of students from B in 2013 = 960
So, Statement I alone is sufficient to answer the question.
From statement II,
Total number of students from B in 2013 = x
Total number of students from B in 2014 = 125x/100 = 5x/4
Total number of students from B in 2015 = 5x/4 * 115/100 = 23x/16
23x/16 – 5x/4 = 480
3x/16 = 480
x = 2560
Total number of students from B in 2013 = 2560
So, Statement II alone is sufficient to answer the question.
8) Answer: A
Total number of students from C in 2013 = x
Total number of students from C in 2014 = x * 130/100 = 13x/10
Total number of students from C in 2015 = 13x/10 * 120/100 = 39x/25
x + 39x/25 = 640
64x = 640 * 25
x = 250
Total number students from C in 2014 = 13 * 250/10 = 325
Total number of students from C in 2015 = 39 * 250/25 = 390
From quantity I,
Number of girls from C in 2014 = 3/5 * 325 = 195
Number of boys from C in 2015 = 195 * 60/100 = 117
Number of girls from C in 2015 = 390 – 117 = 273
From quantity II,
Number of girls from C in 2013 = 2/5 * 250 = 100
Number of boys from C in 2014 = 7/5 * 100 = 140
Number of girls from C in 2014 = 325 – 140 = 185
Quantity I > quantity II
9) Answer: E
From statement I,
Boys from E in 2013, 2014 and 2015=2: 4: 5
Girls from E in 2013, 2014 and 2015=3: 4: 2
So, Statement I alone is not sufficient to answer the question.
From statement II,
Difference between the number of girls from E in 2014 and the number of boys from E in 2015 is 120.
So, Statement II alone is not sufficient to answer the question.
10) Answer: E
From statement I,
Number of students from D in 2013 = 200 + number of students from E in 2013
Ratio of the number of girls to boys from D in 2013 is 3:2.
So, Statement I alone is not sufficient to answer the question.
From statement II,
Ratio of boys to girls from D in 2014 = 5: 7
Number of girls from E in 2015 = 90
So, Statement II alone is not sufficient to answer the question.
| Check Here to View SBI Clerk Mains 2020 Quantitative Aptitude Questions | ||
| Day 09 | Day 08 | Day 07 |
| Click Here for SBI Clerk 2020 – Detailed Exam Notification | ||





