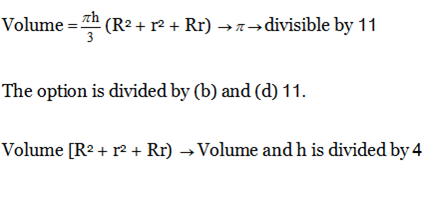Dear Aspirants, Here we have given the Important SSC Exam 2018 Practice Test Papers. Candidates those who are preparing for SSC 2018 can practice these questions to get more confidence to Crack SSC 2018 Examination.
[WpProQuiz 4170]Click here to view Quantitative Aptitude Questions in Hindi
Directions (1-4): The given time graph indicates Income of a firm Study the graph and answers the question-
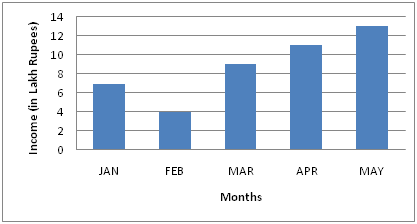
1) Which period shows the steady growth of income?
a) March to May
b) Feb to April
c) February to May
d) The figures are incomplete for estimation
2) During the month, the income ratio Last month’s biggest?
a) February
b) March
c) April
d) May
3) How much is the income from May to February?
a) 25
b) 4
c) 3.5
d) 5
4) Average monthly income of the firm (Rs.)
a) 6
b) 6
c) 8
d) None of these
05) An item is listed at Rs. 65. A customer bought this item for 56.16 rupees and got two consecutive exemptions, the first of which is 10%. The second rate of exemption of this scheme by the shopkeeper was
a) 3%
b) 4%
c) 6%
d) 2%
06) If a principal becomes Q in 2 years, when interest is half yearly in R%. And if the same principal becomes Q in 2 years when interest is S% annually, then which of the following is true?
a) R > S
b) R = S
c) R < S
d) R < D
7) 60 kg of alloy A is mixed with 100 kg of alloy B. If the ratio of alloy A is in 3: 2 and it contains tin and copper, and in alloy B, the ratio 1: 4 contains tin and copper, then the new alloy has tin quantity
a) 36 kg
b) 56 kg
c) 53 kg
d) 80 kg
8)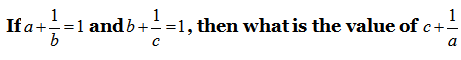
a) 0
b) 2
c) 1
d) 3
09) Point O (O, O), A (8, 0) and B (0, 12) are the vertices of OAB. Tell the circumcircle of OAB
a) (8, 10)
b) (4, 6)
c) (3, 5)
d) None of these
10) If α and β are the roots of equation x2 + 6x + 1 = 0 then what is the value of |α – β|?
11) The sum of all even two digit numbers is divided by one of them leaving no remainder. It is known that the sum of the digits of the divisor is 9, and that the digits in the quotient and divisor are the reverse of each other. The divisor is
a) 18
b) 36
c) 54
d) 72
12)
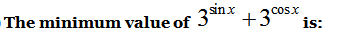
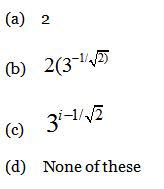
13) Find the product of all the factors of 30.
a) 24 x34 x54
b) 25 x34 x54
c) 24 x36 x54
d) None of These
14) What is the smallest four-digit number that gives the same remainder when divided by any single digit prime numbers?
a) 1051
b) 5051
c) 1510
d) None of these
15) The radius of the circular ends of Rahul’s bucket is 28 centimeters high and 12 centimeters is the capacity of Rahul’s bucket
a) 12684 cm3
b) 1683 cm3
c) 18095 cm3
d) 20064 cm3
Answers :
Direction (1-4) :
1) Answer: a)
This graph clearly shows that the increase in income March to May.
2) Answer: b)
March is more than the month of February
3) Answer: a)
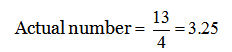
4) Answer: c)
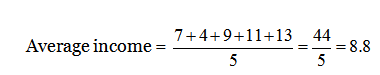
5) Answer: b)
The cost of the article after the first rebate =65 – 6.5 = 5.5
Therefore, second discount
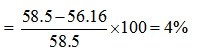
6) Answer: c)
Since interest is collected half yearly on R% per year, the value will be lower than the value of R (Remember, half yearly compounding is always beneficial for the depositor)
7) Answer: b)
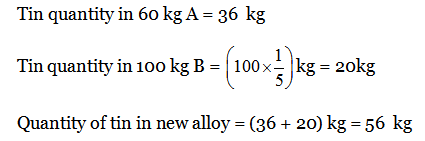
8) Answer: c)
9) Answer: b)
Given, OAB is an equilateral triangle and is the midpoint of the circumcircle of the equal angle.
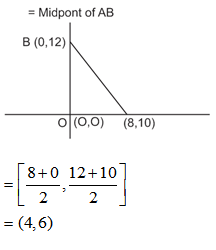
10) Answer :c)
If α and β are the roots of equation x² + 6x + 1 = 0
∴ α and β = − 6 & αβ = 1
Now, (α – β) 2 = (α + β) 2 – 4 αβ
= (-6)² – 4
= 36 – 4 = 32
11) Answer: c)
The sum of all even two digit numbers
= 10 + 12 + 14 + …. + 98
= 2(5 + 6 + 7 + …. + 49)
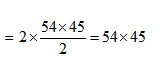
The divisor must be 18, 36 or 54 as it is one of them. It must be 54 for when 54 × 45 is divided by 54, the quotient is 45 and in these, the digits are reversed. So, the divisor must be 54
12) Answer: b)
13) Answer: a)
Method I
Iet we will list down all the factors of 30, these are—
Method I: 1, 2, 3, 5, 6, 10, 15, 30
Now we will write down all these factors in the form of prime factorization
(2o 3o 5o) (21) (31) (51) (21 31) (21 51) (31 51)
= (21+1+1+1) (31+1+1+1) (51+1+1+1)
=24 34 54 = (30)4.
Method II.
30 = 21 × 31 × 51
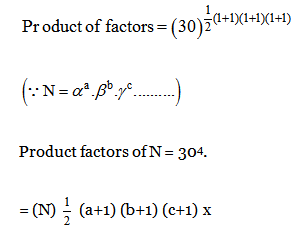
14) Answer: a)
Single digit prime numbers are 2, 3, 5 and 7. Out of them smallest is 2.
It gives only O and 1 as remainders. Hence possible numbers must be in the form of K (LCM of 2, 3, 5 and 7) + 1 or 210 k + 1. So, only options (1) are in this format.
15) Answer: d)