“20-20” Quantitative Aptitude | Crack SBI Clerk 2018 Day-13

By admin - Feb 06 2018

Dear Friends, SBI Clerk 2018 Notification has been released we hope you all have started your preparation. Here we have started New Series of Practice Materials specially for SBI Clerk 2018. Aspirants those who are preparing for the exams can use this “20-20” Quantitative Aptitude Questions. 

[WpProQuiz 1195]

Click “Start Quiz” to attend these Questions and view Explanation

Click Here for SBI Clerk Prelims and Mains 2018 – Full Length Mock Test

1). The ratio of the radii of two right circular cylinders (A and B) is 2 : 5. The ratio of the height of cylinders A to B is 3 : 1. What is the ratio of the volumes of cylinders A to B?

  1. 12:25
  2. 9:25
  3. 9:20
  4. 3:5
  5. 12:35

2). Raja gives 30% of his salary to his mother, 40% of the remaining salary he invests in an insurance scheme and PPF in the ratio of 4 : 3 and the remaining he keeps in his bank account. If the difference between the amount he gives to his mother and that he invests in insurance scheme is Rs.8400, how much is Raja’s salary?

  1. Rs.60,000
  2. Rs.62,000
  3. Rs.64,000
  4. Rs.65,000
  5. Rs.54,000

3). C is 40% less efficient than A. A and B together can finish a piece of work in 10 days. B and C together can do it in 15 days. In how many days can A alone finish the same piece of work?

  1. 18
  2. 12
  3. 14
  4. 20
  5. 15

4). In a bag there are 7 red balls and 5 green balls. Three balls are picked at random. What is the probability that two balls are red and one ball is green in colour?

  1. 29/44
  2. 21/44
  3. 27/44
  4. 23/44
  5. 19/44

5). Shyama invested Rs. P for 2 years in scheme A, which offered 11% pa simple interest. She also invested Rs. 600+P in scheme B, which offered 20% compound interest (compound annually) for 2 years. If the amount received from scheme A was less than that received from scheme B by Rs. 1216 then what is the value of P?

  1. Rs. 1500
  2. Rs. 1400
  3. Rs. 2000
  4. Rs. 1600
  5. Rs. 1800

Directions (Q. 6-10): What approximate value will come in place of question mark (?) in the given questions? (You are not expected to calculate the exact value.)

6). 619.002 – 134.99 ÷ 14.998—(9.01)^2=?

  1. 720
  2. 530
  3. 650
  4. 690
  5. 490

7). 439.97 ÷ 15.02 + 208.08 ÷ 8.01 — 16.01 =?

  1. 120
  2. 60
  3. 100
  4. 80
  5. 40

8) (2914.01 ÷ 31.1) ÷ (1.99 ÷ 3.01) × 510.01 ÷ 169.99 = ?

  1. 405
  2. 423
  3. 340
  4. 452
  5. 567

9). ? % of (140.06 x 7.99 — 679.92) = 330.01

  1. 70
  2. 90
  3. 80
  4. 50
  5. None of these

10). 40% of 859 + 86.01 ÷ 7.99 = ?

  1. 398
  2. 286
  3. 412
  4. 215
  5. 355

Direction (Q. 11-15): Study the following table carefully and answer the questions given below: Number of shirts of different prices bought over the years.

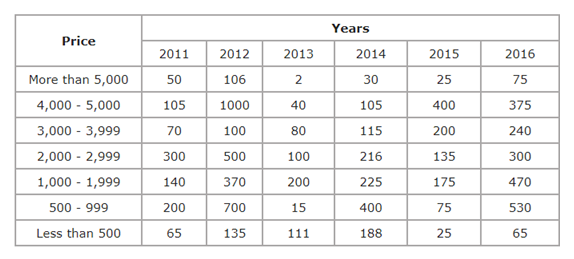
  1. In the price range of 1000 – 1999 the number of shirts bought in 2011 and 2016 together is what percent of the number of shirts bought in 2013 and 2015 in the 2000 – 2999 price range?
  1. 225.95
  2. 259.57
  3. 280.65
  4. 245.78
  5. 266.52
  1. What is the ratio between the number of shirts in price range 4000 – 5000 bought in 2011 and 2015 together and number of shirts in price range 1000 – 1999 bought in 2012 and 2016 together?
  1. 168 : 101
  2. 103 : 174
  3. 91 : 159
  4. 101 : 168
  5. None of these
  1. What is the difference between the number of shirts bought in 2015 and 2016?
  1. 950
  2. 1080
  3. 1020
  4. 1210
  5. 1460
  1. In which year maximum number of shirts was bought?
  1. 2012
  2. 2016
  3. 2014
  4. 2015
  5. None of these
  1. In which price range maximum shirts were bought in the given years taken together?
  1. 500 – 999
  2. 2000 – 2999
  3. 1000 – 1999
  4. 3000 – 3999
  5. None of these

Directions (Q. 16-20): What should come in place of question mark (?) in the following number series:

16).   17,   9,   15,   40,  143.5,   ?

  1. 505.75
  2. 578.5
  3. 650.25
  4. 578
  5. 678.5

17).   3,   5,   13,   49,   241, ?

  1. 1210
  2. 1451
  3. 1221
  4. 1441
  5. 1200

18).   508,   256,   130,   67,   35.5, ?

  1. 18.25
  2. 19.75
  3. 17.25
  4. 15.75
  5. 17.75

19).    7,   13,   31,   85,   247,   ?

  1. 409
  2. 727
  3. 733
  4. 649
  5. 444

20).   64,   36,   22,   15,  ? ,  9.75

  1. 11
  2. 12
  3. 11.5
  4. 11.75
  5. 10

Answers:

1). Answer a

Let the radius of cylinder A be 2x and that of cylinder B be 5x.

Now, height of cylinder A = 3y and height of cylinder B = y

Now, volume of cylinder A = h

= (22/7) x (2x)^2 x 3y = (22/7) x 4x^2 x 3y

Volume of cylinder B = h

= (22/7) × (5x)^2 × y = (22/7) x (25x^2) x y

Required ratio = [ (22/7) x 4x^2 x 3y] / [(22/7) x 25x^2 x y] = 12/25

= 12:25

2). Answer a

Let Raja’s salary be Rs. x.

Raja gives 30% of his salary to his mother.

Raja gives [(x × 30)/100 = Rs. 3x/10] to his mother

Remaining salary of Raja = x – (3x /10) = Rs. 7x /10

Investments of Raja in insurance and PPF is 40% of the remaining salary.

Insurance + PPF = (7x x 40)/ (10×100) = 7x/25

Remaining salary of Raja = 7x/10 – 7x/25

= (35x —14x)/50 = 21x /50

Raja’s investment in insurance scheme

= (7x/25) × (4/7) = 4x/25

Now, according to the question,

3x/10 – 4x/7 = 8400

or, (15x-8x) / 50 =8400

or,  7x = 8400 x 50

x = (8400x 50)/7 =1200 x 50 = Rs. 60000

3). Answer b

Suppose total work = 30 units (LCM of 10 and 15)

(A + B)’s one day’s work = 30/10

= 3 units

And (B + C)’s one day’s work = 30/15 = 2 unit

According to the question, C : A = 60 : 100

or, C :A = 3 : 5

C/A = 3/5

Or, A = 5C/3

Again, A +B = 3 units  ..(i)

B+C = 2 units   …(ii)

Putting the value of A in equation (i), we get

[ 5C/3 + B = 3 unit ] – [B + C = 2 units]

= 5C/3 – C=1 units

Or, 2C/3 = 1 units

C = 3/2 units

Then A = 5C/3 = 5×3/2 / 3 = 2.5 units

Now, total work is 30 units. Then A alone can do the work in

(30 /2.5 =) 12 days

4). Answer b

Total number of balls = 7 + 5 = 12

Now, three halls are picked randomly

Then, the number of sample space n(S)

=12C3 =(10 ×11 ×12) / (1×2×3) = 220

The number of events

n(E) =7C2 x5C1 = [(6×7)/2] x 5

= 21 x 5 = 105

P(E) = n(E)/n(S)=105/220 = 21/44

5). Answer d

Amount received from scheme A

= P+ [(Px2x11)/100] =( 100P+22P)/100 = 122P/100

Amount received from scheme B

= (P + 600) [1+ (20/100)]^2

= (P + 600) (6/5)^2

= (P + 600) (36/25)

= 36P/25 + (600×36)/25 = 36P/25 + 864

Now, according to the question,

36P/25 + 864 – 122P/100 = 1216

Or, 36P/25 – 122P/100 = 1216-864

Or, (144P-122P)/100 = 352

Or, 22P = 352×100

P = (352×100) / 22 = Rs. 1600

Directions (Q. 6-10):

6). Answer b

? = 619.002 – 134.99 ÷ 14.998 –(9.01)^2 = 620 – 135 ÷ 15 – (9)^2

= 620 – 90 = 530

7). Answer e

? = 439.97 ÷ 15.02 + 208.08 ÷ 8.01 –16.01 = 440 ÷ 15 + 208 ÷ 8 – 16

= 29 + 26 – 16 =29 + 10 = 39

8) Answer: b

(2914.01 ÷ 31.1) ÷ (1.99 ÷ 3.01) × 510.01 ÷ 169.99 = ?

94 * (3/2) * (510/170) = X

X= 423

9). Answer e

?% of (140.06 x 7.99 — 679.92) = 330.01

= [? X (140×8-680)] / 100 = 330

or, ? x (1120 — 680) = 330 x 100

or, ? x 440 = 33000

? = 33000 / 440 = 75

10). Answer e

?= 40% of 859 + 86.01 ÷ 7.99

= (40 x 860) / 100  + 86 ÷ 8

= 344 + 11 = 355

Direction (Q. 11-15):

  1. Answer is: b)

Price range of 1000 – 1999 the number of shirts bought in 2011 and 2016

= 140 + 470 = 610

Price range of 2000 – 2999 the number of shirts bought in 2013 and 2015

= 100 + 135 = 235

Required percentage

= 610/235 × 100

= 259.57%

  1. Answer is: d)

Number of shirts in price range 4000 – 5000 bought in 2011 and 2015 together

= 105 + 400 = 505

Number of shirts in price range 1000 – 1999 bought in 2012 and 2016 together

= 370 + 470 = 840

Required ratio = 505 : 840

= 101 : 168

  1. Answer is: c)

Number of shirts bought in 2015

= (25 + 400 + 200 + 135 + 175 + 75 + 25) = 1035

Number of shirts bought in 2016

= (75 + 375 + 240 + 300 + 470 + 530 + 65) = 2055

So required difference = 2055 – 1035

= 1020

  1. Answer is: a)

Number of shirts bought in:

2011 = 50+105+70+300+140+200+65=930

2012 = 106+1000+100+500+370+700+135=2911

2013 = 2+40+80+100+200+15+111=548

2014 = 30+105+115+216+225+400+188=1279

2015 = 25+400+200+135+175+75+25=1035

2016 = 75+375+240+300+470+530+65=2055

So maximum number of shirts was bought in 2012

  1. Answer is: e)

Number of shirts in the price range:

More than 5000 = 50 + 106 + 2 + 30 + 25 + 75 = 288

4000 – 5000 = 105 + 1000 + 40 + 105 + 400 + 375 = 2025

3000 – 3999 = 70 + 100 + 80 + 115 + 200 + 240 = 805

2000 – 2999 = 300 + 500 + 100 + 216 + 135 + 300 =1551

1000 – 1999 = 140 + 370 + 200 + 225 + 175 + 470 = 1580

500 – 999 = 200 + 700 + 15 + 400 + 75 + 530 = 1920

Less than 500 = 65 + 135 + 111 + 188 + 25 + 65 = 589

So maximum number of shirts bought in price range of 4000 – 5000

Directions (Q. 16-20):

16).   Answer c

The series is ×0.5 + 0.5, ×1.5 + 1.5, ×2.5 + 2.5, ×3.5 + 3.5, ×4.5 + 4.5

17).   Answer d

The series is ×2-1, ×3-2, ×4-3, ×5-4, ×6-5

  1. Answer b

The whole series is /2 + 2

19).    Answer c

The logic is, The difference*3

20).   Answer c

The whole series is ×0.5 + 4

Click Here for 20-20 Reasoning Questions for SBI Clerk 2018

0 0 votes
Rating
Subscribe
Notify of
guest
4 Comments
Inline Feedbacks
View all comments
© 2024 All rights reserved. Made with by IBPSGuide